Algebra Tiles

Contents

Description

• Mathematical Concepts
• Connecting Fundamental Math Concepts with Algebra Tiles

Examples

• Integers
• Expressions
• Multiplying Polynomials
• Factoring
• Equations
• Patterning and Functions

Sample Files
Features of the Tool

• Buttons
• Other Functionality

Keyboard Shortcuts
Links

• Videos
  
• PDF Supports
  

Description

The Algebra Tiles Tool is a virtual manipulative similar to the physical Integer and Algebra Tiles commonly available in classrooms. Tiles representing 1, x, x², y ,y² and xy along with their opposites can be dragged into the workspace from the scrollable selection panel at the left. Once in the workspace they can be moved, copied, re-oriented, or negated individually or in groups. The tiles can be configured to match the colours of common physical sets. Unlike the physical tiles, the value of x and y can be adjusted. The virtual tool also contains 1, x, and y line segments.
Access a wide variety of Annotation tools to communicate thinking.
Insert pictures into the tool.
Work created in a mathies tool can be saved and opened. A saved file can be shared with peers or submitted to a teacher. The file will contain all solution steps from start to finish.

Take a screenshot to use as part of a portfolio, presentation, web page, etc.

top

Mathematical Concepts

Algebra Tiles can be used to:

• represent and perform operations on Integers
• represent and perform operations on Polynomials
• simplify algebraic expressions and evaluate algebraic expressions for different values of the variable(s)
• factor polynomials
• solve equations
• explore patterning and functions

top

Connecting Fundamental Math Concepts with Algebra Tiles

Fundamental Concepts and Skills (Link #1)	Algebra Tiles Connections
Working with numbers: Understanding and using numbers (e.g., being able to read, represent, count, order, estimate, compare, compose, decompose, and recompose numbers).	Algebra Tiles can be used to: represent Integers
Recognizing and applying understanding of number properties: Understanding how numbers behave in operations and drawing on that understanding to master math facts and perform calculations.	Algebra Tiles can be used to: relate addition to combining relate subtraction to taking away relate multiplication to repeated addition relate multiplication to an area recognize that the commutative and associative properties apply to the addition and multiplication of integers
Mastering math facts: Understanding and recalling math facts, using a variety of strategies.	Algebra Tiles can be used to: create arrays representing a product of integers e.g., 3 x (-4) apply knowledge of whole number facts to assist in recognizing patterns when operating with integers and polynomials practise number facts while solving problems involving integer and polynomial operations, factoring and solving equations
Developing mental math skills: Doing calculations in the mind, with little or no use of paper and pencil or calculator.	Using visual tools when learning to perform mathematical operations allows students to draw on these mental models and visualizations to perform mental calculations. Students will develop their mental math skills with Algebra Tiles as they: solve problems involving the addition, subtraction and multiplication of integers and polynomials relate factoring to division of polynomials
Developing proficiency with operations: Performing calculations with ease, precision, and consistency and with a general understanding of number and operations, number properties, and their appropriate application in problem solving.	Algebra Tiles can be used to: recognize the inverse relationship between addition and subtraction e.g., since 5 + (–3) = 2, then 2 – (–3) = 5 recognize the inverse relationship between multiplication and division e.g., since (x + 1)(x + 2) = x2 + 3x + 2, then (x2 + 3x + 2) ÷ (x + 2) = (x + 1). solve equations by checking various substituted values

Connecting Fundamental Math Concepts with mathies.ca (Draft)

top

Examples

Integers

Integers can be represented by using the 1 and -1 tiles (or segments). Arithmetical operations can be performed by manipulating two or more representations.

A 1 tile can be dragged from the selection panel at the left onto the workspace. The multiplier button at the bottom right of the selection panel can be used to bring 1, 2, 5, or 10 tiles onto the workspace at a time. Existing tiles can be copied to create additional tiles in the workspace.

If you select some 1 tiles, a negate button appears which can be used to change them to -1 tiles. Alternatively, the negate button at the bottom left of the selection panel can be used to show the opposites of tiles and segments in that panel, which can then be dragged to the workspace.

In the example below, at the bottom of the workspace, the multiplication question 3 x (-4) is represented using an array model showing 3 rows of -4 tiles .

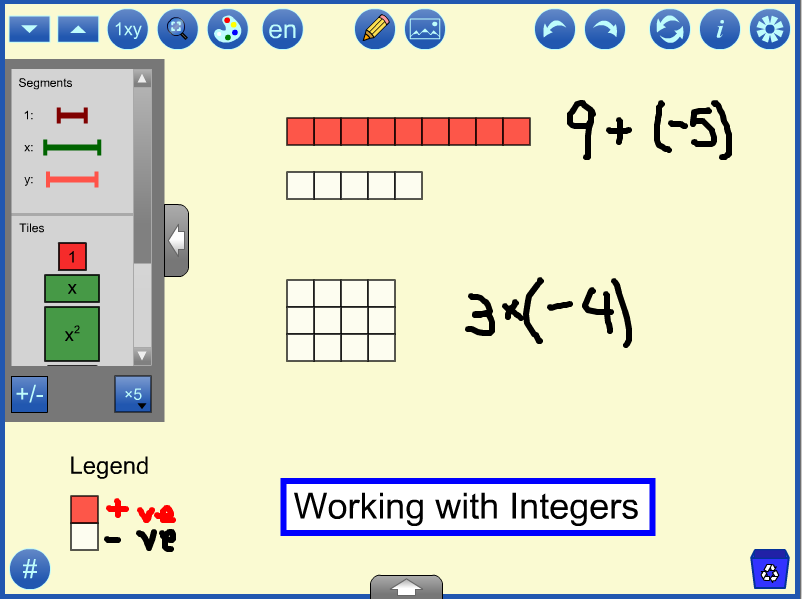
The addition at the top of the workspace, 9 + (-5), can be performed by combining the nine 1 tiles and the five -1 tiles. Using the tool, select the five -1 tiles and move them on top of the nine 1 tiles, the tool will “poof” the five opposites, leaving four 1 tiles. Each 1 and -1 pairing is referred to as a "zero pair".

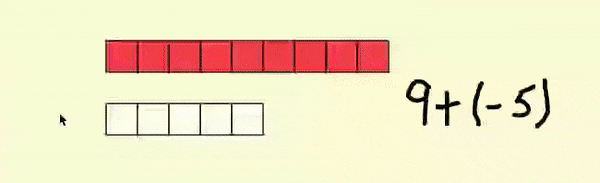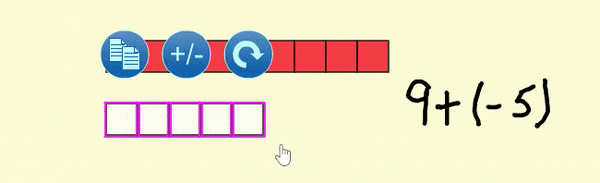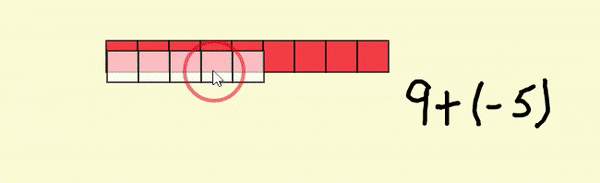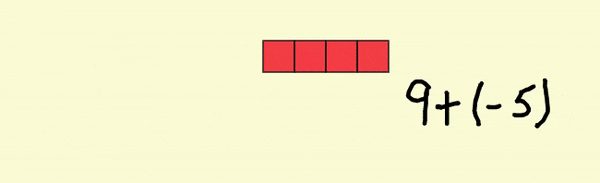
If you open Sample File 1 and press the redo button twice , you will see the result of “poofing” the zero pairs.

A legend is supplied to establish the colour being used for 1 and -1. These colours can be changed in the tool by:

• clicking on a tile or segment in the selection panel at the left and choosing a new colour from the palette.
• clicking the colour palette button at the top of the screen and choosing one of six common colour sets provided.

Note:

• Settings are found by clicking the Gear icon , including a setting that:
  • determines if zero pairs are automatically removed.
  • changes the transparency of the background grid.
• The values panel at the bottom of the screen can be hidden (click the arrow to show/hide it again).
• The annotation tools on the right are shown by clicking the pencil icon and can be hidden or shown using the arrow on its panel.

top

Expressions

Algebraic expressions can be represented using tiles or segments. Arithmetical operations can be performed by manipulating these representations. Expressions related to area and perimeter of rectangles can be modelled directly.

Adding expressions can be thought of as combining tiles. In the example below, the tiles are combined in an order that allows them to be renamed as 8x + 2y + 4. This is a powerful visual image of what it means to 'simplify by collecting like terms'.

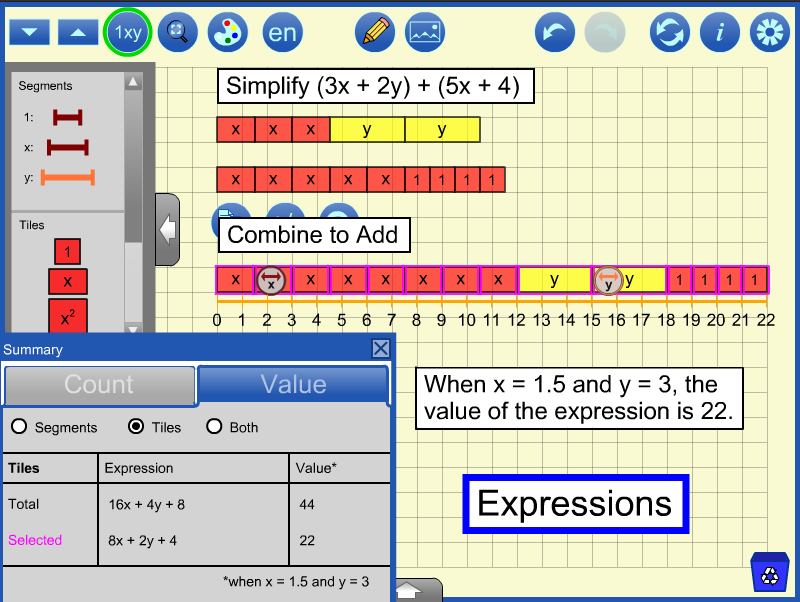
Expressions can be evaluated at specific variable values. In the example above, a number line is used to measure the length of the rectangle after x has been set to 1.5 and y to 3. Notice that each x tile measures 1.5 on the number line and each y tile measures 3 units.

The Summary dialog is shown when is clicked. Clicking on the dialog's Value tab will allow the work to be verified. The combined tiles are selected and the value of the selected tiles is listed as 22, which agrees with the measurement. Students might be asked to explain why the value of the total is twice as big as the selected and how the expression for the total reinforces that conclusion. See Sample File 2.

By default, opposite tiles poof (disappear) when combined, extending the "zero-pair" principle for Integers to algebraic terms. Students might be asked to represent 3x – 4 in at least six different ways.

top

Multiplying Polynomials

Polynomials can be multiplied using an area model. A rectangle is formed with dimensions equal to the two factors. The product of the two factors is represented by the area of the rectangle and is expressed in terms of the variables in the dimensions, as in the two examples below.

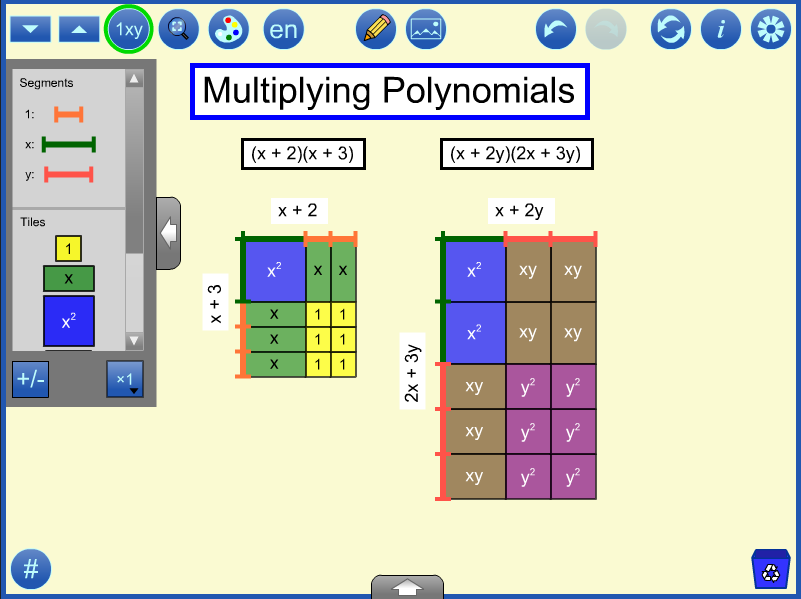
Segments can be used to create the dimensions of the rectangle to be filled in.

          

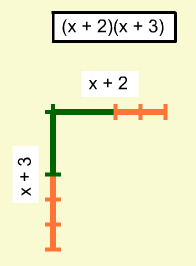
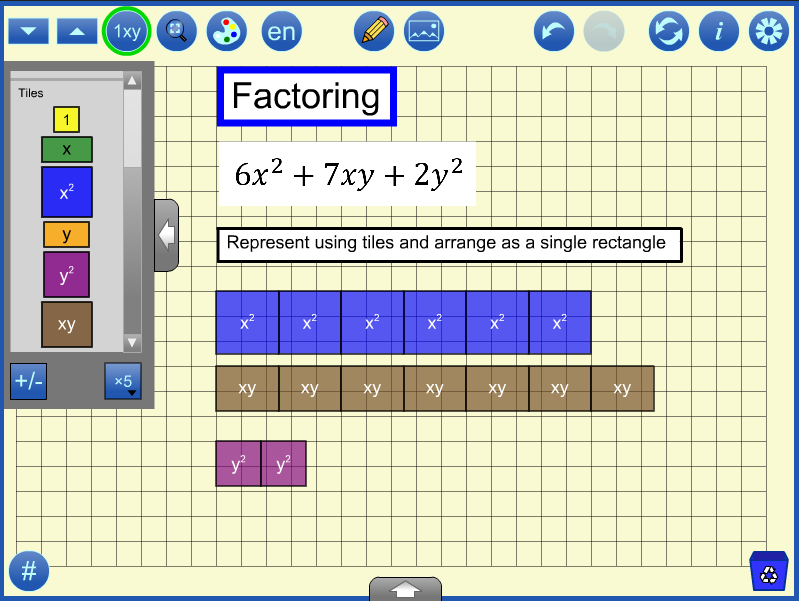
Once the tiles are used to fill in the area, the values of the variables should be adjusted to show that the rectangular area represents the correct product for every value of the variable(s) not just specific instances. Then an expression for each product can be determined. Here the products are x² + 5x + 6 and 2x² + 7xy + 6y². Students might be asked what is the same and different about the two multiplication questions.

top

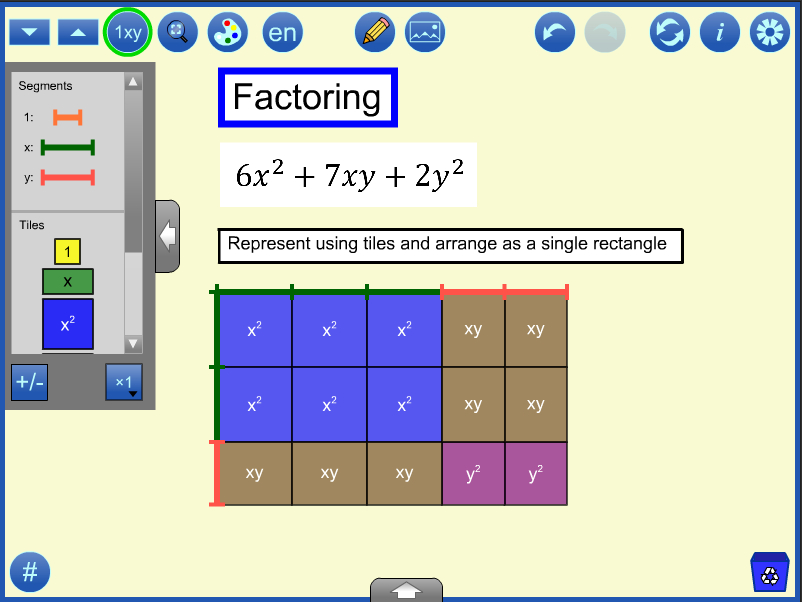
Factoring

Factoring is the inverse operation of multiplying in that the polynomial is expressed as a multiplication of two or more factors. When using an area model, this involves arranging the tiles representing the polynomial into a single rectangle. To do this with the Algebra Tiles tool, represent the polynomial then drag the tiles to form a single rectangle. Identify the dimensions of that rectangle as the factors of the polynomial.

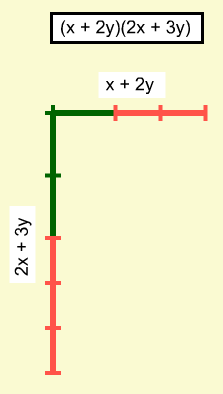
Once the rectangle is formed, segments can be used to mark off the dimensions which are used as factors in the result, (3x + 2y)(2x + y). The variable values should be adjusted to demonstrate that the factors are the same for rectangles of varying sizes. (If you open sample file 4 and click redo repeatedly, you will see this).

top

Solving Equations

Equations can be represented using tiles or segments and solved by trial and error or by balancing.

In the trial and error example below, the equation is modeled using segments. A number line from the annotation tools is used to mark off 10 units. The value of x is changed by sliding the controller on the workspace or in the values panel at the bottom of the screen, until the length is 10 units. (If you open sample file 5 and click redo, you will see this).

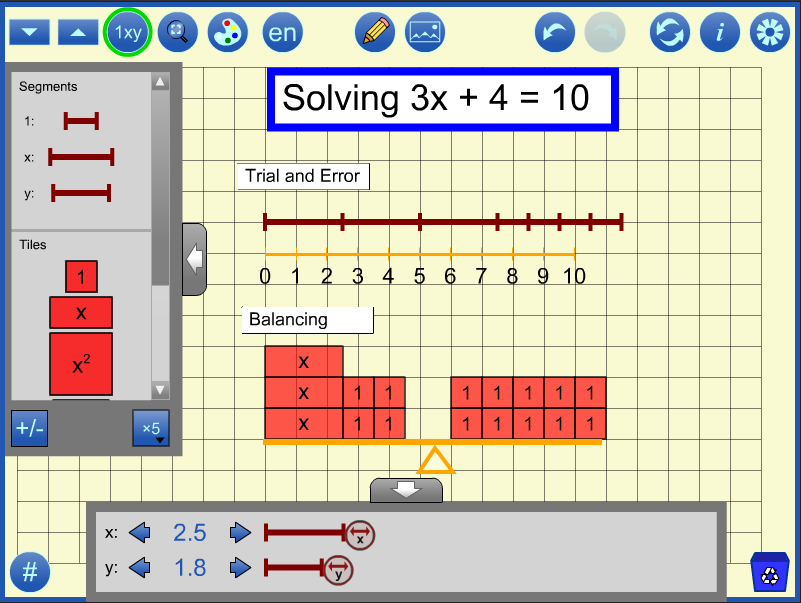
A balance is drawn using the annotation tools, and tiles are used to represent the equation. Using the principle that equal quantities can be added or removed, 4 is removed from both sides (or -4 added and poofed). The six remaining unit tiles on the right are then arranged in 3 groups of 2 to match the left side in order to conclude that x = 2 (If you open sample file 5 and continue to click redo, you will see how this might be performed using the tool).

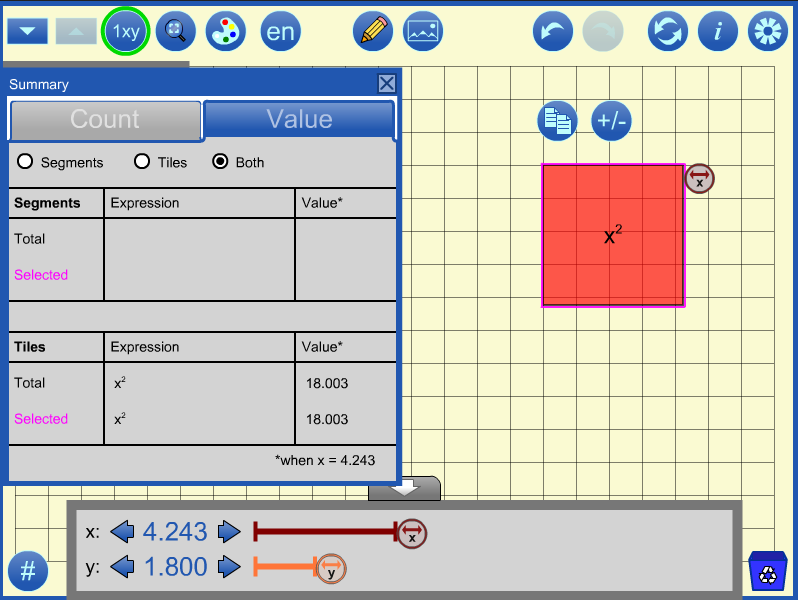
In the example below, the equation x² = 18 is solved to find the principal square root of 18. The summary panel allows you to see the value of x² as x changes. Change the number of decimal places in the settings from 1 to 2 to 3 decimal places to get a finer and finer approximation.

Trial and Error can also be used to solve a system of equations like:
2x + y = 15,
x + 3y = 20

top

Patterning and Functions

Algebra tiles can be used to explore various patterns and related functions.
For example, consider the expression (x + 1)².
This expression can be represented using algebra tiles.

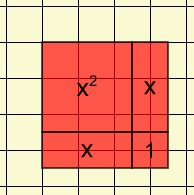
This image shows the representation using the default value of x = 2.5. Physical manipulatives are designed using an x value of approximately 5.2. Both of these instances illustrate the expression at one particular value. However, the advantage of using the mathies Algebra Tiles tool is that the value of x can be adjusted.

When x = 1, the representation is made up of 4 unit squares so the value of the expression is 4.

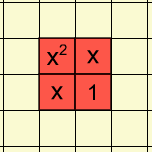
How does the representation change as the value of x increases?

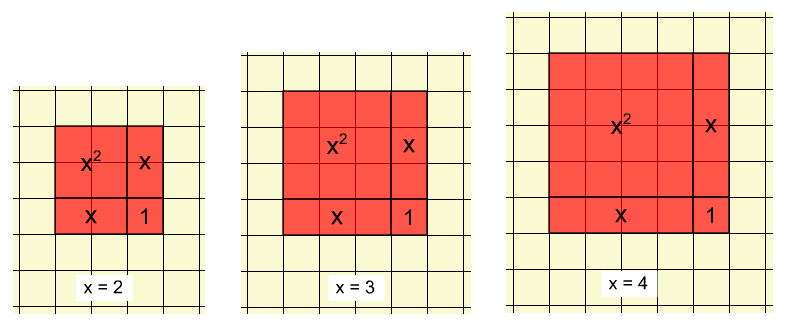
Notice that for each value of x, the representation forms a square with side lengths (x+1). As the value of x changes, the side lengths change, the areas of the x and x² tiles change and the 1 tile remains constant.

The value of the expression for each value can be determined algebraically and can be confirmed either by counting the grid squares or showing the value tab of the summary dialog . e.g., when x = 3, the value of the expression (x + 1)² is 16.

Each of these representations can be thought of as a term of a pattern or a point on a graph. The annotation tools can be used to created a table of values and/or a graph.

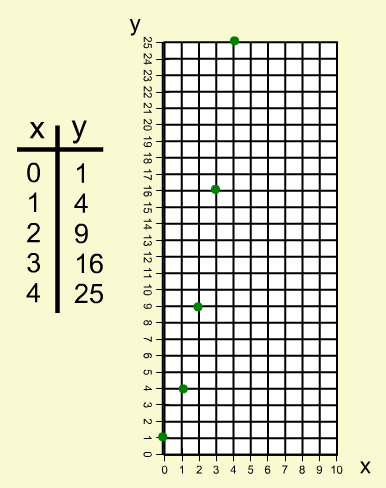
The function y = (x + 1)² is of course a continuous function. Values in between the integral points can also be illustrated using the tool.

top

Sample Files

To access a sample file:

• click the link in the Sample column (desktop only), or
• use the Open WWW button in the Settings dialog and supply the URL, or
• download the file from the URL column (right-click and save locally on desktop, hard tap on mobile) and use the Open button in the tool.
• add the mathies sample files Google drive folder to "My Drive" which allows convenient access on all devices.

See the File Operations page for more details.

Sample Click to open in the tool - desktop only	URL Type or copy into Open WWW text box, or save locally by right-clicking or hard-pressing
Working with Integers	https://mathies.ca/files/examples/AT_Ex1.xml
Working with Expressions	https://mathies.ca/files/examples/AT_Ex2.xml
Multiplying Polynomials	https://mathies.ca/files/examples/AT_Ex3.xml
Factoring Polynomials	https://mathies.ca/files/examples/AT_Ex4.xml
Solving Equations	https://mathies.ca/files/examples/AT_Ex5.xml

Note: These files were designed on a desktop computer and may not open exactly as shown on other devices.

top

Features of the Tool

Button	Description
	Unit Size Decrease / increase the size of a unit tile.
	Labels Hide / show the labels on the tiles in the workspace.
	Size to Fit Adjust the values of x and y to the maximum values that will still allow objects to fit on the stage.
	Choose Colour Set Shows a dialog with options to select any of the six predetermined colour sets.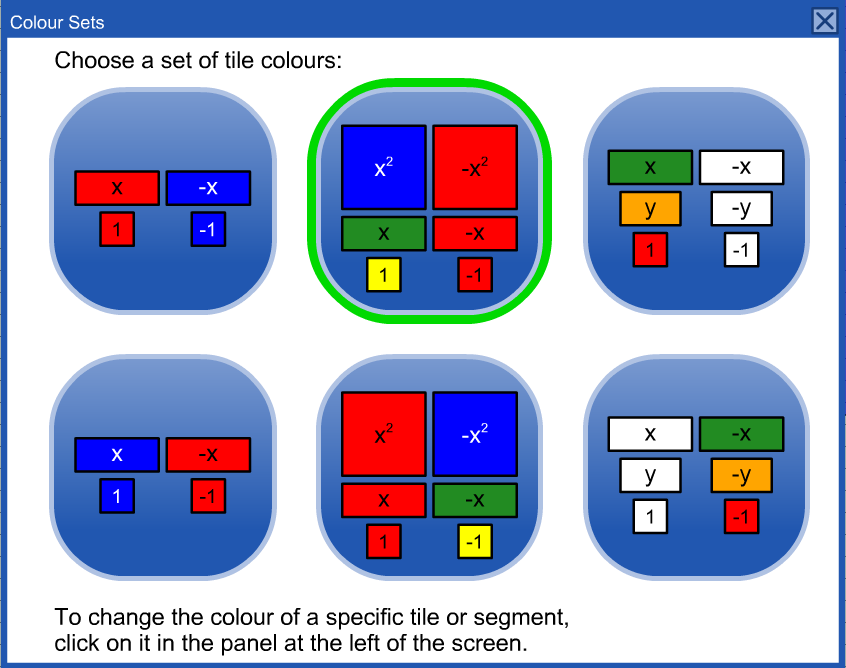
	English / French Switch between English and French.
	Annotation Tool Hide / Show a wide variety of Annotation Tools which can be used to communicate thinking.
	Insert Image Button Insert images into the tool. More details.
	Undo / Redo Step backward or forward through the actions taken with the tool. This feature is not only useful for backtracking when a misstep is made, it enables a student to demonstrate their work from the start to the finish. The student can press Undo until they are at the start of their solution and then click Redo repeatedly, explaining each step. Note: Undo / Redo is not available for annotation objects.
	Reset Delete all work and return the tool to its starting state.
	Information Shows a dialog with a link to this support page, a feedback form as well as copyright details and version number.
	Settings Shows the settings dialog. Select the number of decimal places used for values of x and y. This setting is useful when evaluating expressions or solving equations. Remove zero pairs controls whether or not opposites will poof (disappear) when tiles in the workspace overlap. The Auto Size Annotation setting is selected by default. This means that if the unit size is changed, any annotation in the workspace will be scaled to match. Open, Import and Save files (see File Operations for more details)
	Negate Button Show the opposites of the tiles and segments in the selection panel.
	Number of Copies to Drag Set the number of copies to drag from the selection panel.
	Summary Shows the summary dialog which contains a Count and a Value tab. Each tab shows information about the objects in the workspace. Separate entries occur for the total workspace and for those objects which are currently selected. The option buttons at the top can be set to show details about only the segments, only the tiles or both the segments and the tiles. The Count tab shows a summary of the number of each type of tile. The Value tab shows an algebraic expression and its value when evaluated at the given values of x and y.
	Recycle (in the workspace) Click to clear selected objects. If nothing is selected, the entire workspace will be cleared. Alternatively, drag items to the recycle bin to remove them.
	Copy Make a copy of the selected objects.
	Negate Selected Change the selected tiles and segments in the workspace to their opposites.
	Change Orientation Change the selected tiles and segments from horizontal to vertical and vice versa.

top

Other Functionality

	Multiple Select To select objects draw a marquee rectangle around them. Hold down the SHIFT key when drawing a marquee rectangle to add to the previous selection. Click an object to add or remove it from the selection. Selected objects can be moved, copied, negated, re-oriented, or recycled as a group.
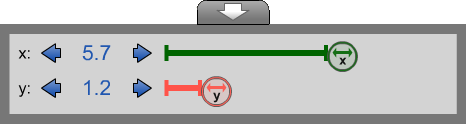	Adjusting Values The values panel is shown to the left. The value(s) of the variable(s) can be adjusted by: dragging the thumbs found on the selected objects in the workspace (see image in the Multiple Select row above) dragging the thumbs on the line segments found in the values panel clicking the steppers found in the values panel typing a value in the stepper text box in the values panel
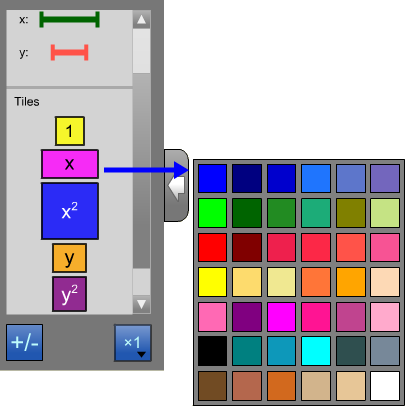	Configure the Selection Panel Click on a tile or segment in the selection panel to change the colour of all objects of that type.

top

Keyboard Shortcuts

On the desktop version of this tool, the standard Keyboard Shortcuts have been implemented.
In the Algebra Tiles tool,
SPACE + R is used to change the orientation of selected tiles from horizontal to vertical and vice versa.

Links

Videos

The following videos demonstrate how algebra tiles can be used.

1. Simplifying Algebraic Expressions
2. Balancing Equations
3. Using the Area Model to Model Multiplication and Factoring of Algebraic Expressions

(Source - EduGAINS /Ministry Developed Resources /Mathematics /Classroom Practices /Lessons & Supports /Manipulatives)

PDF supports

1. Focusing on the Fundamentals of Math - A Teacher's Guide
2. Connecting Fundamental Math Concepts with mathies.ca (Draft)
3. A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles This document contains a collection of lessons which use algebra tiles to explore concepts. Worked examples and student work sheets are included.
4. Algebra Tiles
   (Source - EduGAINS /Ministry Developed Resources /Mathematics /Classroom Practices /Lessons & Supports /Manipulatives)
   
   • What are Algebra Tiles?
   • How do Algebra Tiles help students?
   • How many are recommended?
   • Sample Activities
   • Recommended Websites
   
   Visit EDUGAINS for additional manipulative Tip Sheets.
   

top