|
|
||||||
 |
|
pour communiquer la pensée.
dans l'outil.
et ouverts*
.
Un fichier enregistré peut être partagé avec des pairs ou soumis à un enseignant / une enseignante. Le fichier contiendra toutes les étapes de la solution dès le début jusqu'à la fin.| Fundamental Concepts and Skills (Lien #1) | Les tuiles algébriques et les liens aux concepts fondamentaux |
|---|---|
| Développer le sens du nombre : comprendre et utiliser les nombres (c.-à-d. pouvoir lire, compter, dénombrer, représenter, ordonner, estimer, comparer, composer, décomposer et recomposer des nombres). |
Les tuiles algébriques peuvent être utilisées pour :
|
| Reconnaître et utiliser les propriétés des opérations : comprendre les propriétés des opérations afin de développer des stratégies efficaces pour maîtriser les faits mathématiques et effectuer des calculs. |
Les tuiles algébriques peuvent être utilisées pour :
|
| Maîtriser les faits numériques : comprendre et se rappeler des faits numériques, en ayant recours à des stratégies de rappel variées. |
Les tuiles algébriques peuvent être utilisées pour :
|
| Développer les compétences en calcul mental : effectuer mentalement des calculs sans l’aide, ou presque, de papier-crayon et de calculatrices. |
L'utilisation d'outils visuels lors de l'apprentissage d'opérations mathématiques permet aux élèves de s’appuyer sur ces modèles et visualisations mentales pour effectuer des calculs mentaux. Les élèves vont développer les compétences en calcul mental à l'aide des tuiles algébriques lorsqu'ils :
|
|
Développer le sens des opérations : effectuer des calculs de manière efficiente, avec efficacité et précision et en démontrant une bonne compréhension des faits numériques, des propriétés des opérations et de leur application à la résolution de problèmes. |
Les tuiles algébriques peuvent être utilisées pour :
|
Relier les concepts fondamentaux en mathématiques avec mathies.ca (brouillon)
Les nombres entiers peuvent être représentés en utilisant les tuiles (et les segments) 1 et -1. Les opérations arithmétiques peuvent être effectuées en manipulant deux représentations ou plus.
Une tuile de la valeur 1 peut être déplacée du panneau de sélection à gauche sur l'espace de travail. Le bouton de multiplicateur 
en bas à droite du panneau de sélection peut être utilisé pour importer 1, 2, 5 ou 10 tuiles à la fois sur l'espace de travail. Les tuiles existantes peuvent être copiées pour créer des tuiles supplémentaires.
Si vous sélectionnez des tuiles d'une valeur de 1, un bouton pour changer sa valeur à son opposée 
apparaît. En appuyant sur ce bouton les tuiles de la valeur 1 deviennent -1. Vous pouvez également utiliser le bouton 
situé en bas à gauche du panneau de sélection pour afficher les tuiles ou les segments opposés dans le panneau avant des déplacés vers l'espace de travail.
Dans l'exemple ci-dessous, au bas de l'espace de travail, la question de multiplication 3 x (-4) est représentée à l'aide d'une disposition rectangulaire montrant 3 rangées de -4 tuiles.
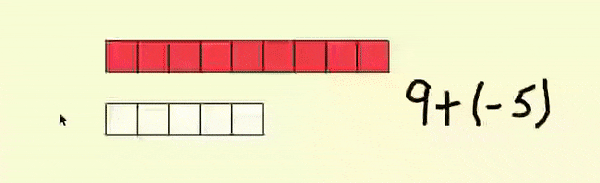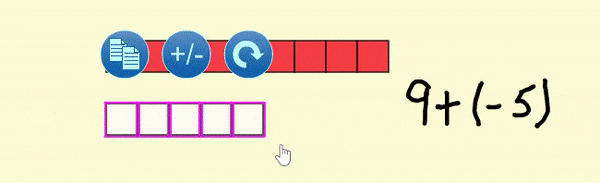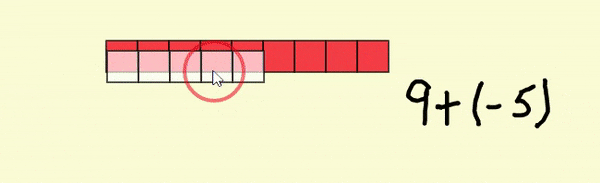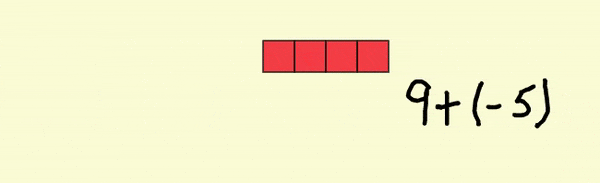
L'addition en haut de l'espace de travail, 9 + (-5), peut être effectuée en combinant les neuf tuiles d'une valeur de 1 et les cinq tuiles, chacune d'une valeur de -1. À l'aide de l'outil, sélectionner les cinq tuiles de -1 et placer les au-dessus des neuf tuiles positives. L'outil va automatiquement faire disparaître les cinq tuiles de valeurs opposées laissant quatre tuiles. Chaque paire de 1 et -1 sont appelé "paire nulle".
Si vous ouvrez l'échantillon de fichier 1 et que vous appuyez deux fois sur le bouton de rétablir 
, vous verrez le résultat du “pouf” des paires nulles.
Une légende est fournie pour établir la couleur utilisée pour 1 et -1. Ces couleurs peuvent être changées dans l'outil en :
en haut de l'écran et en choisissant un des six ensembles de couleurs prédeterminées.
, y compris un paramètre qui :
et peuvent être cachés ou affichés à l'aide de la flèche sur son panneau.Les expressions algébriques peuvent être représentées à l'aide de tuiles ou de segments. Les opérations arithmétiques peuvent être effectuées en manipulant ces représentations. Les expressions liées à l'aire et au périmètre des rectangles peuvent être modélisées directement.
L'addition des expressions peut être considérée comme une combinaison de tuiles. Dans l'exemple ci-dessous, les tuiles sont combinées dans un ordre permettant de les renommer 8x + 2y + 4. Ci-dessous est une image de ce que signifie 'simplifier en rassemblant des termes semblables'.
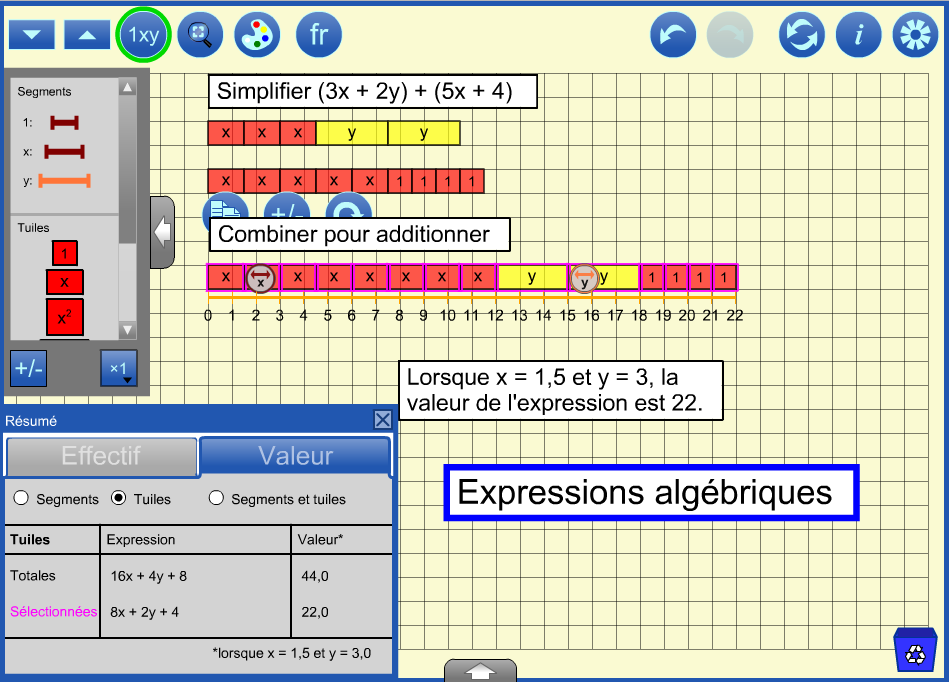
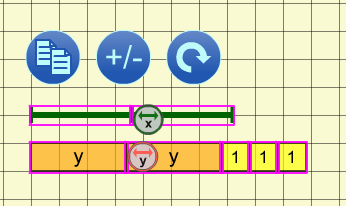
Les expressions peuvent être évaluées avec des valeurs de variables spécifiques. Dans l'exemple ci-dessus, une droite numérique est utilisée pour mesurer la longueur du rectangle une fois que x a été défini sur 1,5 et y sur 3. Noter que chaque tuile de x mesure 1,5 sur la droite numérique et chaque tuile d'y mesure 3 unités.
La boîte de dialogue Résumé s'affiche lorsque vous cliquez sur le bouton 
. En cliquant sur l'onglet Valeur de la boîte de dialogue, le travail pourra être vérifié. Les tuiles combinées sont sélectionnées et la valeur des tuiles est 22, ce qui correspond à la mesure. On pourrait demander aux élèves d'expliquer pourquoi la valeur du total est deux fois plus grande que celle sélectionnée et en quoi l'expression du total renforce cette conclusion. Voir le fichier d'échantillon 2.
Par défaut, les tuiles opposées disparaissent (pouf!) lorsqu'elles sont combinées, étendant le principe de "paire nulle" pour les nombres entiers aux termes algébriques. Les élèves peuvent être invités à représenter 3x – 4 d'au moins six manières différentes.
Retour en hautLes polynômes peuvent être multipliés à l'aide d'une disposition rectangulaire. Un rectangle est formé avec des dimensions égales aux deux facteurs. Le produit des deux facteurs est représenté par l'aire du rectangle et est exprimé en matière de variables dans les dimensions, comme dans les deux exemples ci-dessous.
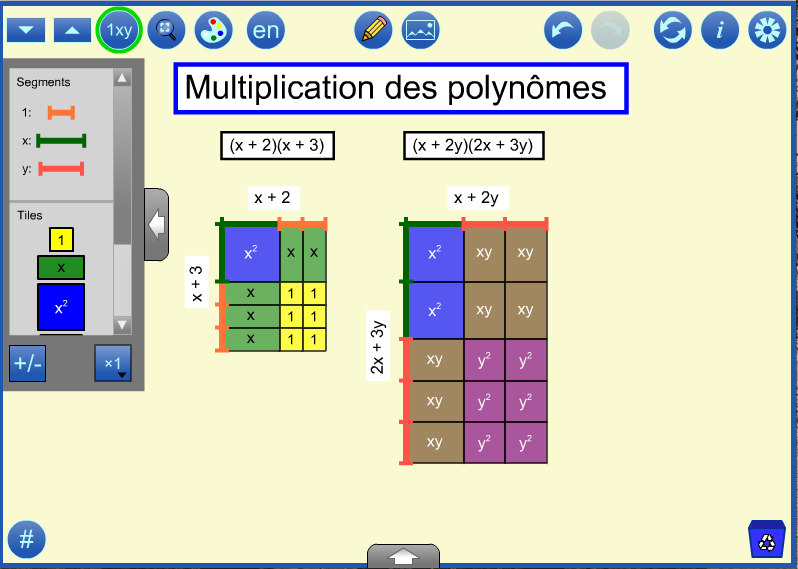
Les segments peuvent être utilisés pour créer les dimensions du rectangle à remplir.
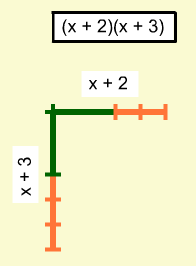
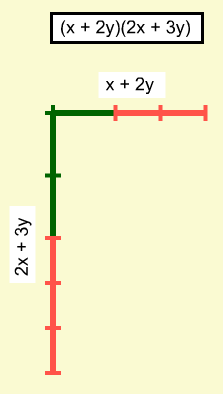
Une fois que les tuiles sont utilisées pour remplir l'aire de la surface, les valeurs des variables doivent être ajustées pour indiquer que l'aire de la surface rectangulaire représente le produit correct pour chaque valeur d'une ou des variables et pas uniquement pour des instances spécifiques. Ensuite, une expression pour chaque produit peut être déterminée. Ici, les produits sont x2 + 5x + 6 and 2x2 + 7xy + 6y2. On pourrait demander aux élèves en quoi les deux questions de multiplication sont identiques et différentes.
Retour en hautLa factorisation est l'opération inverse de la multiplication en ce sens que le polynôme est exprimé comme une multiplication de deux ou plusieurs facteurs. Lorsqu'on utilise un modèle de surface de disposition rectangulaire, il s'agit d'organiser les tuiles représentant le polynôme en un seul rectangle. Pour ce faire avec l’outil Tuiles algébriques, représenter le polynôme, puis faire glisser les tuiles pour former un seul rectangle. Identifier les dimensions de ce rectangle en tant que facteurs du polynôme.
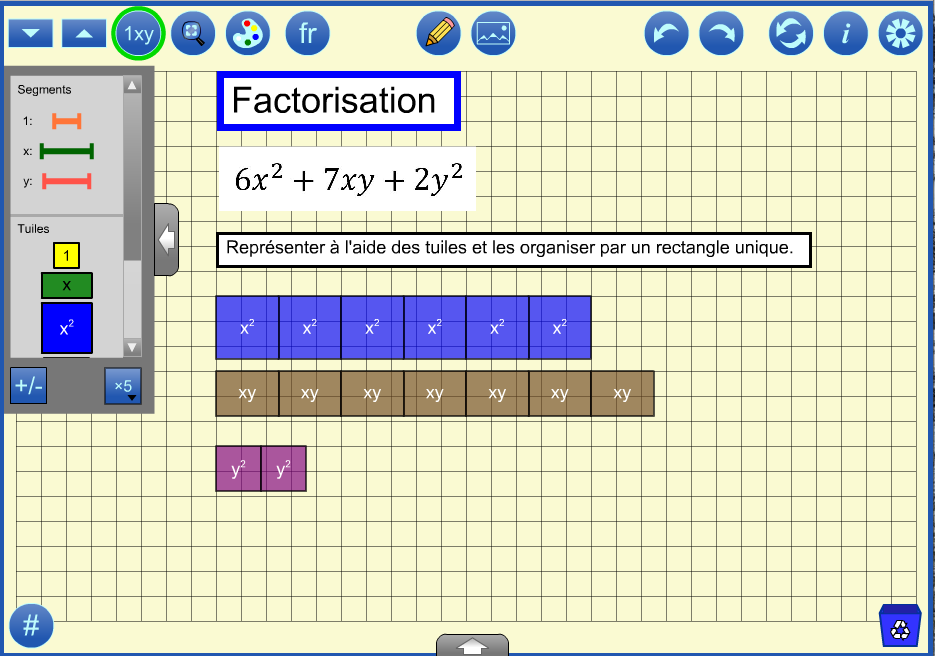
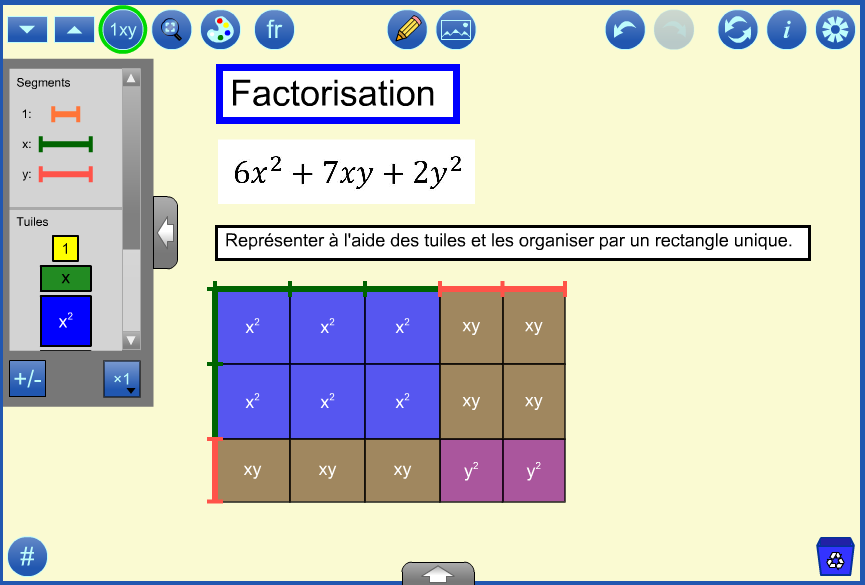
Une fois que le rectangle est formé, des segments peuvent être utilisés pour marquer les dimensions qui sont utilisées comme facteurs dans le résultat (3x + 2y)(2x + y). Les valeurs des variables doivent être ajustées pour démontrer que les facteurs sont les mêmes pour les rectangles de tailles différentes. (Si vous ouvrez le fichier d’échantillon 4 et vous cliquez le bouton rétablir à plusieurs reprises, vous verrez ceci).
Les équations peuvent être représentées à l'aide de tuiles ou de segments et être résolues par essais et erreurs ou par la mise en équilibre.
Dans l'exemple d'essais et d'erreurs, ci-dessous, l'équation est modélisée à l'aide de segments. Une droite numérique des outils d'annotation est utilisée pour marquer 10 unités. La valeur de x est modifiée en faisant glisser le curseur sur l'espace de travail ou dans le panneau de valeurs en bas de l'écran jusqu'à ce que la longueur soit de 10 unités. (Si vous ouvrez le fichier échantillon 5 et vous cliquez sur le bouton rétablir, vous verrez ceci).
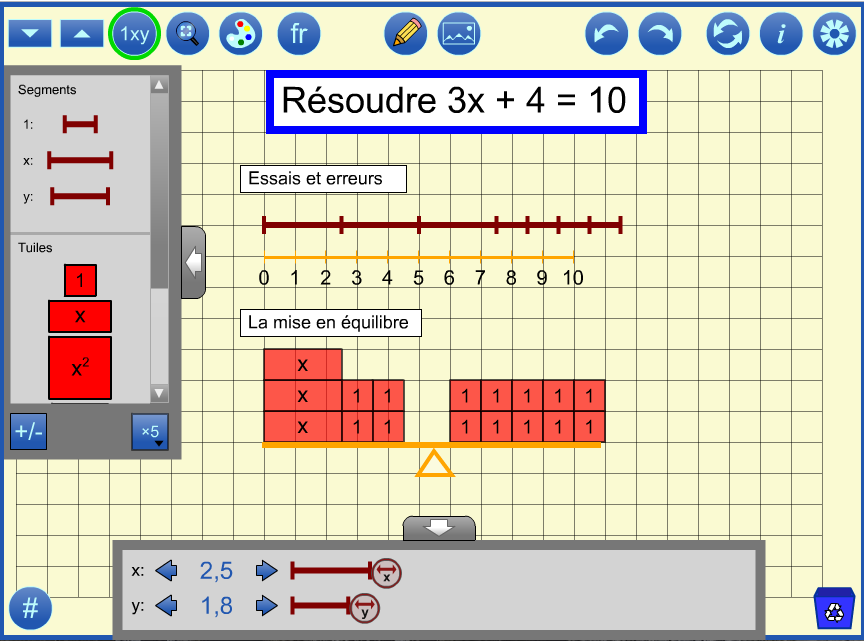
Une balance est dessinée à l'aide des outils d'annotation, et des tuiles sont utilisées pour représenter l'équation. En utilisant le principe que des quantités égales peuvent être ajoutées ou retirées, 4 sont retirées des deux côtés (ou -4 sont ajoutés et pouf, disparraissent). Les restes des six tuiles d'unité sur la droite sont ensuite disposés en 3 groupes de 2 pour correspondre au côté gauche afin de conclure que x = 2. (Si vous ouvrez le fichier d'échantillon 5 et vous cliquer le bouton rétablir à plusieurs reprises, vous verrez comment cela peut être effectué à l'aide de l'outil).
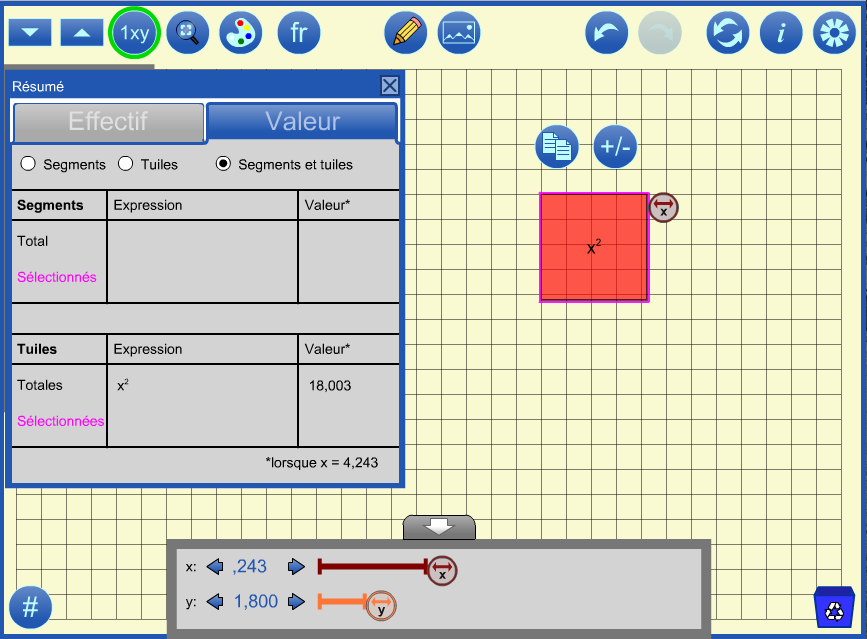
Dans l'exemple ci-dessous, l'équation x2 = 18 est résolue pour trouver la racine carrée principale de 18. Le panneau de résumé vous permet de voir la valeur de x2 lorsque x change. Modifier le nombre de décimales dans les paramètres de 1 à 2 à 3 positions decimales pour obtenir une approximation de plus en plus fine.
Essais et erreurs peuvent également être utilisés pour résoudre un système d'équations tel que :
2x + y = 15,
x + 3y = 20
Les tuiles algébriques peuvent être utilisées pour explorer divers concepts de régularité et de fonction.
Par exemple, considérons l'expression (x + 1)2.
Cette expression peut être représentée à l'aide de tuiles algébriques.
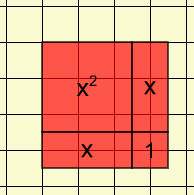
Cette image montre la représentation en utilisant la valeur par défaut de x = 2,5. Le matériel de manipulation est conçu en utilisant une valeur x d'environ 5,2. Ces deux exemples illustrent l'expression à une valeur particulière. Cependant, l’avantage d’utiliser l’outil mathies Tuiles algébriques est que la valeur de x peut être ajustée.
Lorsque x = 1, la représentation est composée de 4 unités carrées de sorte que la valeur de l'expression est 4.
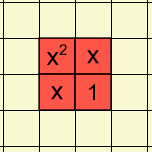
Comment la représentation change-t-elle lorsque la valeur de x augmente ?
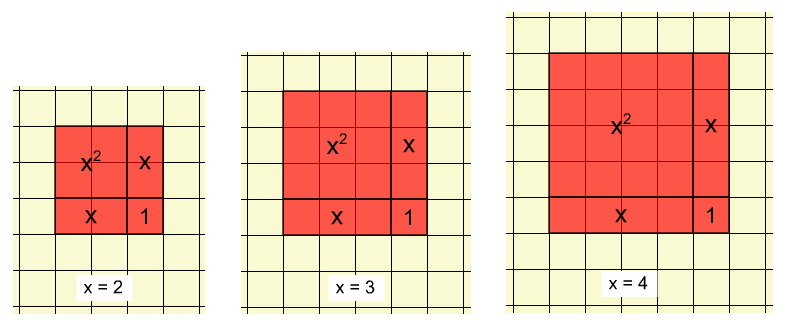
Noter que pour chaque valeur de x, la représentation forme un carré avec des côtés de longueur (x+1). Lorsque la valeur de x change, les longueurs des côtés changent, l'aire des tuiles x et x2 change et la tuile 1 reste constante.
La valeur de l'expression pour chaque valeur peut être déterminée algébriquement et confirmée en comptant les carrés du quadrillage ou en affichant l'onglet de valeur de la boîte de dialogue résumé . Par exemple, lorsque x = 3, la valeur de l'expression (x + 1)2 est 16.
Chacune de ces représentations peut être considérée comme le terme d'une régularité ou d'un point sur un graphique. Les outils d'annotation peuvent être utilisés pour créer une table de valeurs et / ou un graphique.
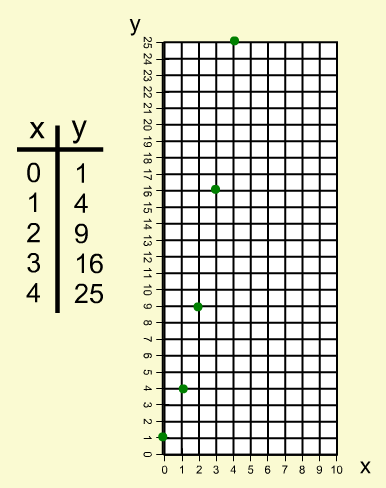
La fonction y = (x + 1)2 est bien entendu une fonction continue. Les valeurs entre les points d'intégration peuvent également être illustrées à l'aide de l'outil.
Retour en haut
dans la boîte de dialogue Paramètres et indiquer l'URL, ou
dans l'outil, ou
ÉchantillonsCliquer pour ouvrir l'outil - ordinateur de bureau uniquement |
URLTaper ou copier dans la zone de texte Ouvrir WWW, ou enregistrer localement en cliquant avec le bouton droit de la souris ou en appuyant fort. |
|
Travailler avec des entiers
|
https://mathies.ca/files/examples/AT_Ex1fr.xml |
|
Travailler avec des expressions
|
https://mathies.ca/files/examples/AT_Ex2fr.xml |
|
Multiplication des polynômes
|
https://mathies.ca/files/examples/AT_Ex3fr.xml |
|
Factorisation des polynômes
|
https://mathies.ca/files/examples/AT_Ex4fr.xml |
|
Résolution des équations
|
https://mathies.ca/files/examples/AT_Ex5fr.xml |
| Boutons | Descriptions |
 |
La taille de l'unitéDiminuer / Augmenter la taille des blocs mosaïques géométriques. |
 |
ÉtiquettesCacher / afficher les étiquettes sur les tuiles de l'espace de travail. |
 |
Zoom pour adapterAjuster les valeurs de x et y aux valeurs maximales permettant aux objets de rester sur l'espace de travail. |
|
|
Choisir un ensemble de couleursAfficher une boîte de dialogue avec des options pour sélectionner l’un des six ensembles de couleurs prédéterminées. |
  |
Anglais/FrançaisPasser de l'anglais au français et vice-versa. |
|
|
Outil d’annotationCacher / Montrer une grande variété d'outils d'annotation qui peuvent être utilisés pour communiquer la pensée. |
 |
Insérer une imageInsérer des images dans l'outil. Plus de détails. |
 |
Annuler/RétablirReculer ou avancer dans les actions avec l’outil. Cette fonctionnalité est non seulement utile pour revenir en arrière quand un faux pas est fait, mais permet également aux étudiants et étudiantes de démontrer leur travail dès le début jusqu'à la fin. Les élèves peuvent appuyer sur Annuler jusqu’à ce qu’ils soient au début de leur solution, puis appuyer sur Rétablir à plusieurs reprises pour expliquer chaque étape. Remarquer : Annuler/Rétablir n'est pas disponible pour les objets d'annotation. |
 |
RéinitialiserSupprimer tout le travail et ramener l'outil à son état de départ. |
 |
InformationsAccéder à un lien vers une page de support, un formulaire de rétroaction, ainsi que les informations de droit d’auteur et le numéro de version. |
|
|
ParamètresAfficher la boîte de dialogue Paramètres. Sélectionner la position de décimale utilisée pour les valeurs x et y. Ce paramètre est utile pour évaluer des expressions ou de résoudre des équations. Le paramètre de supprimer les paires nulles contrôle si les opposés disparaissent ou non lorsque les tuiles sur l'espace de travail se chevauchent. Le paramètre d'ajuster automatiquement la taille de l'annotation est sélectionné par défaut. Cela signifie que si la taille de l'unité est modifiée, toute annotation sur l'espace de travail sera mise à l'échelle pour correspondre. Ouvrir, importer et enregistrer des fichiers (voir Opérations de fichiers* pour plus de détails disponibles en anglais seulement). |
|
|
Choisir l'objet opposéAfficher les tuiles et les segments opposés dans le panneau de sélection. |
 |
Nombre de copies à faire glisserDéfinir le nombre de copies à faire glisser à partir du panneau de sélection. |
|
|
RésuméAfficher la boîte de dialogue Résumé contenant l'onglet Effectif et l'onglet Valeur
 L'onglet Valeur affiche une expression algébrique et sa valeur lorsqu'elle est évaluée aux valeurs données de x et y. |
 |
Supprimer(tout sur l'espace de travail)Cliquer pour supprimer les objets sélectionnés. Si rien n'est sélectionné, tout l'espace de travail sera effacé.
|
 |
CopierFaire une copie des objets sélectionnés. |
|
Choisir l'opposé d'objets sélectionnésRemplacer les tuiles et les segments sélectionnés sur l'espace de travail par leurs opposés. |
 |
Changer l'orientationChanger l'orientation des tuiles et des segments sélectionnés d'une position horizontale à verticale et vice-versa. |
 |
Sélection multiplePour sélectionner des objets, cliquer et faire glisser le curseur pour créer un rectangle de sélection autour d'eux.Pour ajouter à la sélection précédente, créer un rectangle de sélection en maintenant la touche Maj enfoncée. Cliquer l'objet pour l'ajouter ou le supprimer de la sélection. Les objets sélectionnés peuvent être déplacés, copiés, changés à leurs opposés, réorientés ou supprimés en tant que groupe. |
 |
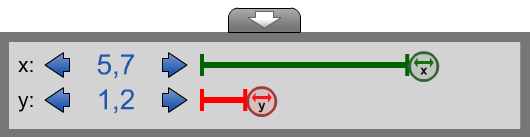Ajuster les valeursLe panneau de valeurs est situé au bas de l'espace de travail.La ou les valeurs de la ou des variables peuvent être ajustées comme suit :
|
 |
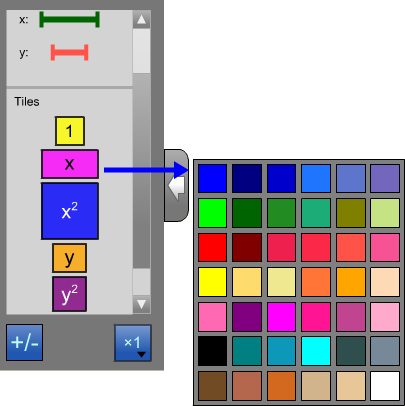Modifier le panneau de sélectionCliquer sur une tuile ou un segment dans le panneau de sélection pour modifier la couleur de tous les objets de ce type. |
Bandes de fractions
Bloc-notes
Blocs mosaïques géométriques+
L'outil d'ensemble
Monnaie
Réglettes+
Rekenrek
Tableau des nombres
Tuiles algébriques
Tuiles de couleur
attachés aux objets sélectionnés sur l'espace de travail (voir l'image dans la rangée de sélection multiple ci-dessus)