Description
Exemples
Fonctionnalités
Liens
Tableau des nombres
L'outil interactif de mathies comprend deux tableaux (0-99 et 1-100), un tableau des additions (jusqu'à 12 + 12) et un tableau des multiplications (jusqu'à 12 x 12). Retourner des cartes individuelles, des rangées ou des colonnes au complet ou retourner toutes les cartes à la fois.
Considérations relatives au tableau des nombres
- Zéro n'est pas un nombre à compter. Donc, le tableau 1-100 pourrait être préféré pour des activités de dénombrement.
- Zéro est un nombre à part entier, pas seulement un chiffre dans des valeurs telles que 50. Le fait de définir 0 comme première valeur du tableau 0-99 permet de souligner ce fait.
- Tous les nombres de chaque décennie apparaissent dans la même rangée (p. ex., 20, 21, 22, ...29) sur le tableau des nombres 0 à 99. Les valeurs d'une rangée donnée contiennent tout le même chiffre de dizaines et un chiffre d'unité. En voyant toutes les valeurs de la même décennie dans la même rangée renforcera le concept de la valeur de position.
- Sur les deux tableaux, en déplaçant un carré à la droite, on peut dire que c'est la même que d'additionner 1, tandis qu'en déplaçant un carré à la gauche est de soustraire 1.
- Sur les deux tableaux, en déplaçant d'une rangée directement vers le bas d'une valeur donnée est la même que d'additionner 10, tandis qu'en déplaçant une rangée vers le haut d'une valeur donnée est de soustraire 10.
- Des questions telles que 16 - 16 peuvent être résolues à l'aide du tableau 0-99, mais pas du tableau 1-100.
- Des questions telles que 86 + 14 peuvent être résolues à l'aide du tableau 1-100, mais pas du tableau 0-99.
- Voir lien #3 pour plus de détails.
Concepts de mathématiques
Les tableaux des nombres offrent plusieurs manières d'explorer de nombreuses compétences en mathématiques, telles que :
- le dénombrement
- les régularités
- le développement et la compréhension des stratégies d'addition
- le développement et la compréhension des stratégies de multiplication
- la résolution de problèmes
Les tableaux d'addition et de multiplication offrent des possibilités de rétroaction immédiate au fur et à mesure que les élèves pratiquent des faits d'addition et de multiplication. Ces tableaux peuvent également être utilisés pour aider les élèves à développer et à comprendre diverses stratégies d’addition et de multiplication.
L’apprentissage des élèves peut être adapté de différentes manières, ce qui permet de répondre à divers besoins d’apprentissage (par exemple, cacher des rangées et des colonnes pour prendre en compte moins de cartes).
Prendre une
capture d'écran pour partager votre travail ou pour l'ajouter à votre portfolio.
Retour en haut
Établissement des liens entre les concepts fondamentaux en mathématiques et le tableau des nombres
| Les compétences et concepts fondamentaux (lien #6) |
Tableau des nombres et les liens aux concepts fondamentaux |
Développer le sens du nombre :
comprendre et utiliser les nombres (c.-à-d. pouvoir lire, compter, dénombrer, représenter, ordonner, estimer, comparer, composer, décomposer et recomposer des nombres).
|
Les tableaux des nombres peuvent être utilisés pour :
|
Reconnaître et utiliser les propriétés des opérations :
comprendre les propriétés des opérations afin de développer des stratégies efficaces pour maîtriser les faits mathématiques et effectuer des calculs. |
Les tableaux des nombres et des opérations peuvent être utilisés pour :
|
Maîtriser les faits numériques :
comprendre et se rappeler des faits numériques, en ayant recours à des stratégies de rappel variées. |
Les tableaux d'opérations sont des bons outils d'apprentissage pour mettre en pratique des faits d'addition et de multiplication.
|
Développer les compétences en calcul mental :
effectuer mentalement des calculs sans l’aide, ou presque, de papier-crayon et de calculatrices.
|
L'utilisation d'outils visuels lors de l'apprentissage d'opérations mathématiques permet aux élèves de s'appuyer sur ces modèles et visualisations mentales pour effectuer des calculs mentaux.
Le tableau des nombres peut être utilisé pour mettre en pratique diverses stratégies, notamment :
- de décomposer des nombres en beaux nombres pour faciliter les calculs
- d'effectuer la compensation en ajoutant puis en soustrayant le même montant
|
Développer le sens des opérations :
effectuer des calculs de manière efficiente, avec efficacité et précision et en démontrant une bonne compréhension des faits numériques, des propriétés des opérations et de leur application à la
résolution de problèmes.
|
Les élèves peuvent utiliser les tableaux d'opérations pour reconnaître et utiliser la relation inverse entre l’addition et la soustraction (p. ex., puisque 4 + 5 = 9, alors 9 – 5 = 4) ainsi que la relation inverse entre la multiplication et la division (p. ex., puisque 7 x 8 = 56, alors 56 ÷ 7 = 8).
|
Relier les concepts fondamentaux en mathématiques avec mathies.ca (brouillon)
Retour en haut
Exemples
Dénombrement
Les tableaux des nombres peuvent être utilisés pour aider les élèves à développer des compétences relatives aux nombres.
Développer le sens du nombre à l'aide d'un tableau des nombres de 1-100
-
Demander aux élèves de déterminer les nombres manquants sur le tableau.
-
Pour modifier le niveau de difficulté, demander aux élèves de travailler avec plusieurs rangées.
-
Demander aux élèves de marquer chaque numéro (ici, le timbre circulaire est utilisé) lorsqu'ils comptent par intervalles autres que 1.
Encourager les élèves à rechercher des régularités.
-
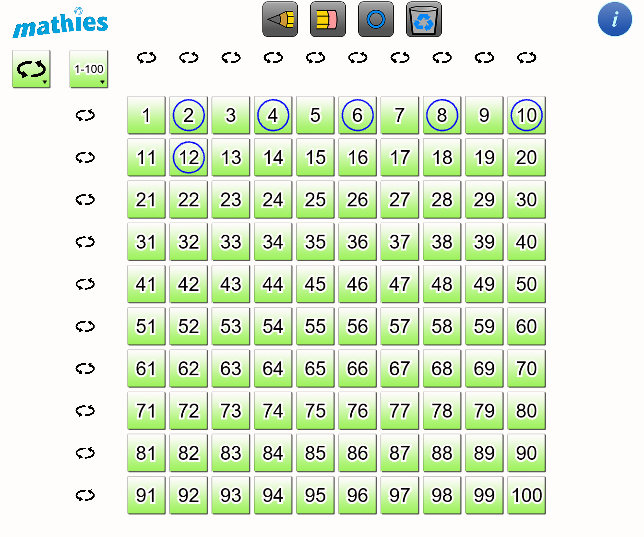
Encourager les élèves à compter par intervalles autrement qu'à partir des nombres respectifs 1, 2, 5 ou 10 afin de visualiser les changements de régularités.
L'exemple ci-dessous est de compter par intervalles de 5 à partir de 3.
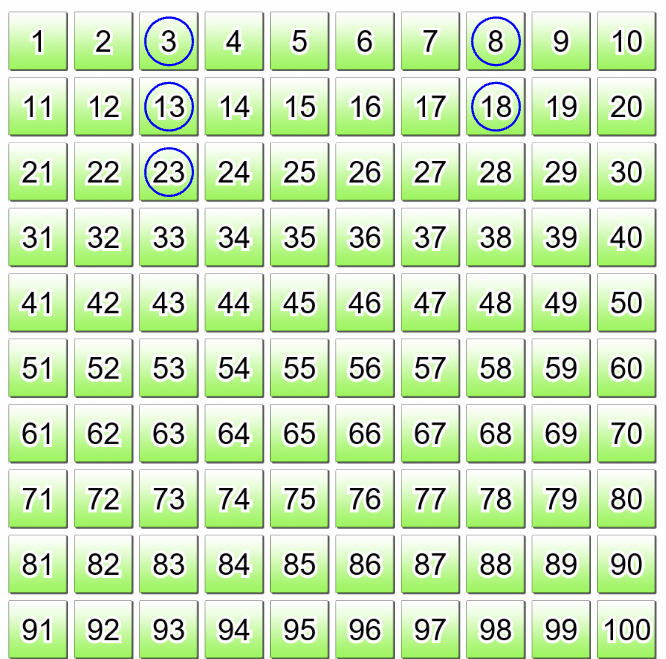
Retour en haut
Régularités
Les tableaux peuvent être utilisés pour créer une gamme de motifs tels que des motifs AB simples à des motifs croissants ou décroissants. De plus, les élèves peuvent approfondir leur compréhension des multiples. Les élèves peuvent utiliser les tableaux pour identifier, développer et créer des régularités.
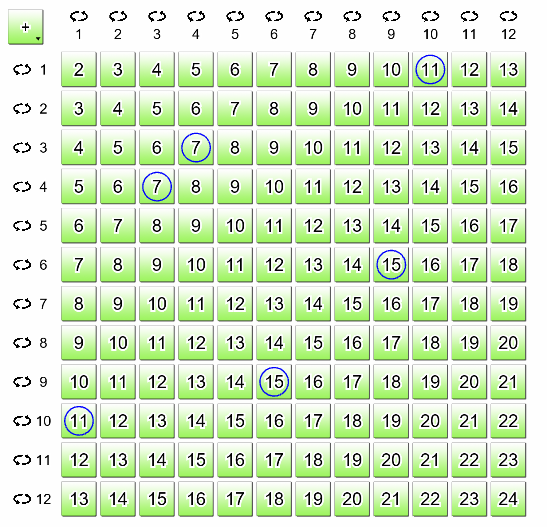
Reconnaître les régularités des nombres à l'aide du tableau des nombres 0-99
- Retourner tous les nombres avec un 3 dans la valeur de position des unités et des dizaines. Chercher une régularité. Répéter cet exercice avec le nombre 7 et faire la comparaison au nombre 3. Essayer ceci avec d'autres nombres. Qu'est-ce qui se produit ? Pourquoi ?
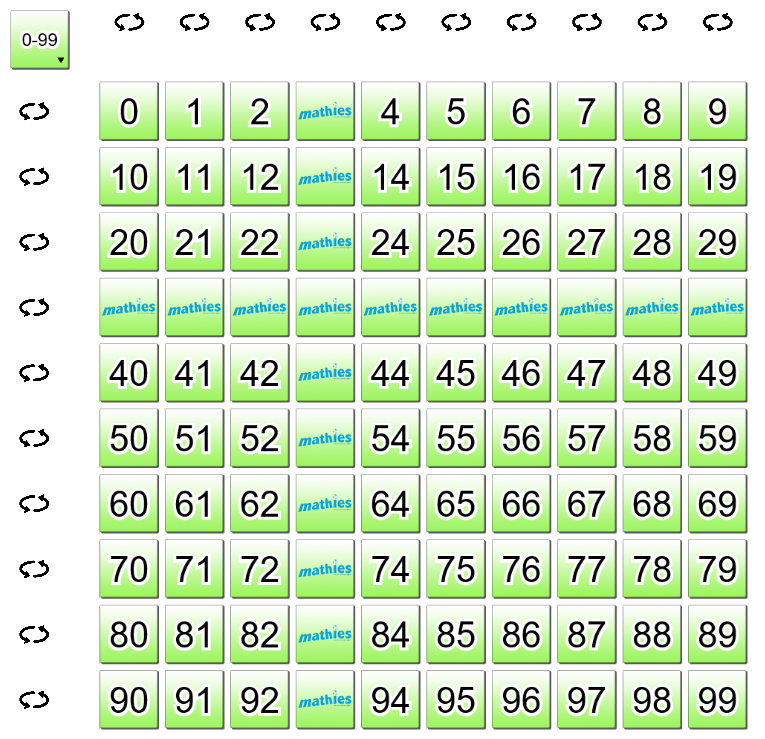
- Jouer avec des défis. Cacher tous les nombres avec :
- des chiffres qui additionnent à 9,
- un chiffre des dizaines plus grand que le chiffre des unités,
- un chiffre des dizaines plus petit que le chiffre des unités.
Reconnaître les régularités des nombres à l'aide des tableaux des nombres 0-99 ou 1-100
-
Cacher la face de toutes les cartes. Retourner deux cartes à faces visibles, laisser la prochaine carte à face cachée, retourner à faces visibles les deux cartes qui suivent et finalement, laisser à face cachée une autre carte. Demander aux élèves de continuer la suite numérique à motif répété. Peuvent-ils prédire quelles valeurs seront les cartes faces cachées avant de les retourner ? Lorsque la régularité est prolongée jusqu'à la fin du tableau des nombres, demander aux élèves de réfléchir aux valeurs des cartes qui restent faces cachées. Les élèves peuvent ensuite utiliser l'option Tout retourner pour retourner toutes les cartes. Demander aux élèves d'essayer un motif répété différent et à rechercher les régularités.
-
Donner des défis de régularités aux élèves à marquer sur leurs tableaux. Demander leurs de déterminer la règle des suites et d'identifier les nombres qui suivent. Par exemple, 19, 16, 13, 10… ou 21, 28, 35, 42…
-
Considérer les diagonales dans le tableau 0-99.
Quelles régularités remarquez-vous ? Considérer les diagonales dans le tableau 1-100. Quelles régularités remarquez-vous ? Comment les régularités sont-elles les mêmes ? Différentes ? (Adapté du lien #3)
Retour en haut
Additions
Activités d'additions à l'aide des tableaux des nombres 0-99 ou 1-100
- Considérer une régularité impliquant le déplacement d'une rangée de dix vers le bas ou le haut à partir d'une valeur donnée puis se déplacer d'une ou deux cases vers la droite ou la gauche (c'est-à-dire l'addition ou la soustraction de 11 ou 12). Aider les élèves à établir des liens à leurs compétences en calcul mental.
- Calculer la somme de 23 + 36 en décomposant des termes pour créer des beaux nombres (des nombres facilement manipulables). Utiliser la stratégie de faire des dizaines et des unités. Par exemple, décomposer le nombre 36 pour créer 30 + 6.
Additionner 23 + 30 en procédant comme suit: commencer à 23 sur le tableau d'addition, descendre trois rangées de dix, puis se déplacer de 6 cases vers la droite.
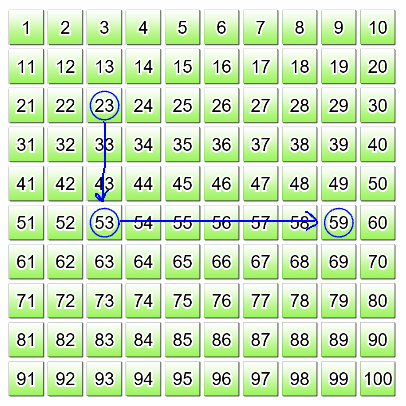
- Calculer la somme des nombres telle que 38 + 8. Utiliser la stratégie de la compensation dans l'addition (additionner d'un côté et puis soustraire le même montant de l'autre).
Exemple,
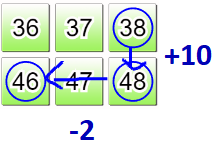
- penser à 38 + 8
- comme 38 + (8 + 2) - 2
- ou 38 + 10 - 2.
- Démontrer la propriété d'associativité de l'addition.
Par exemple, démontrer que la somme des termes (7 + 6) + 4 a le même résultat que 7 + (6 + 4).
Activités des faits numériques à l'aide d'un tableau d'addition
- Discuter explicitement de diverses stratégies d'addition (source : lien #4). Indiquer les termes d'additions où ces stratégies s'appliquent sur le tableau. Certains faits d'addition supplémentaires peuvent être déterminés à l'aide de plusieurs stratégies. Rechercher des régularités visuelles pour chaque stratégie.
- 1 de plus et 2 de plus (p. ex., 5 + 1 et 7 + 2)
- Utilisation des doubles (p. ex., 2 + 2 et 8 + 8)
- Les voisins des doubles ou les doubles plus un (p. ex., 6 + 7 et 5 + 4)
Cette stratégie implique des sommes lorsqu'un des termes d'addition est un de plus que l'autre terme.
La stratégie consiste à doubler le plus petit nombre et à en ajouter 1 ou à doubler le plus grand nombre et à en enlever 1.
- 10 comme point d'ancrage (p. ex., 1 + 9 et 8 + 2)
- Regroupement par dizaines - "Faire 10" (p. ex., 3 + 8 et 9 + 5)
Dans ces faits numériques de base, l’un des termes est 8 ou 9. Selon le cas, les élèves ajoutent 1 ou 2 provenant de l’autre terme pour obtenir 10, et lui ajoutent ce qui reste de cet autre terme.
Par exemple, pour le fait 9 + 5, commencer par 9 et emprunter 1 du terme 5 pour faire 10. Ensuite additionner 4 qui est le montant restant pour obtenir la somme de 14.
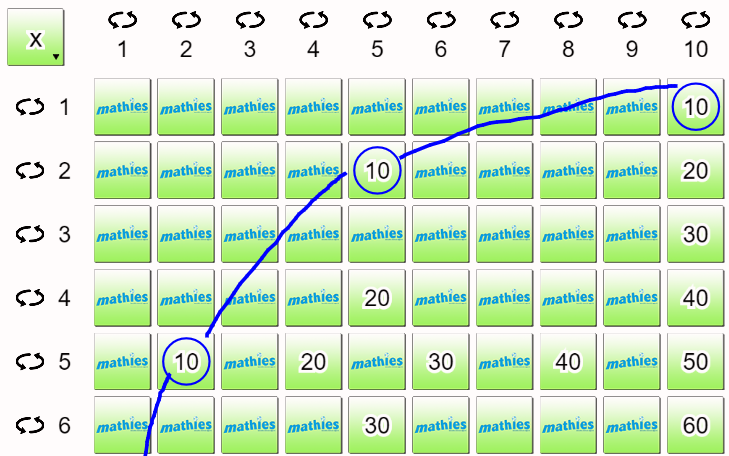
- Démontrer la propriété de la commutativité de l'addition
Dans l'exemple ci-dessous, les paires de questions sont marquées : 3 + 4 et 4 + 3, 1 + 10 et 10 + 1, 9 + 6 et 6 + 9.
Marquer plusieurs autres paires de questions sur le tableau d'addition. Quelle régularité remarquez-vous ?
- Combien de façons différentes pouvez-vous trouver deux nombres qui additionnent à 12 ? Marquer chaque somme sur le tableau d'addition. Répéter en utilisant une somme différente. Quelles régularités remarquez-vous ?
- Pratiquer des faits d'addition.
Commencer avec toutes les cartes à faces cachées. Choisir un fait d'addition. Déterminer la somme. Retourner la carte correspondante pour vérifier.
Retour en haut
Multiplications
Utiliser un des
tableaux des nombres, attribuer un nombre et demander aux élèves de trouver et de retourner ce nombre et ses multiples.
Activités des faits numériques à l'aide d'un tableau de multiplication
- Rechercher des régularités liées à divers facteurs. Commencer avec des multiples de 2, 5, et 10 et additionner progressivement les autres facteurs. Décriver la régularité pour chaque facteur trouver sur le tableau de multiplication.
- Cacher tous les nombres du tableau. Concentrez-vous sur un facteur en considérant une ligne ou une colonne à la fois. Exposer certains des numéros (produits) et déterminer chacun des produits manquants. Retourner la carte pour vérifier. Penser aux stratégies utilisées. Discuter.
Par exemple, considérer les produits pour lesquels un facteur est 6. Les produits 6, 12, 30 et 60 sont affichés. Déterminer les multiples restants de 6.
- Cacher tous les nombres du tableau. Sélectionner au hazard un chiffre entre 0 et 9. Retourner toutes les cartes de produit contenant un chiffre correspondant au chiffre sélectionné de manière aléatoire. Discuter : comment savez-vous que vous avez trouvé tous les produits contenant le chiffre indiqué ? Quelles stratégies avez-vous utilisées ? (Source : lien #1)
- Démontrer la propriété de la commutativité de la multiplication.
Marquer des paires de questions telles que : 3 x 4 et 4 x 3, 1 x 10 et 10 x 1, 9 x 6 et 6 x 9.
Marquer plusieurs autres paires de questions sur le tableau de multiplication. Quelle régularité remarquez-vous ?
- Démontrer la propriété de l'associativité de la multiplication.
Par exemple, démontrer où le produit des facteurs (3 x 2) x 5 a le même résultat que 3 x (2 x 5).
- Pratiquer les faits de multiplication.
Commencer avec toutes les cartes à faces cachées. Choisir un fait de multiplication. Déterminer le produit. Retourner la carte correspondante pour vérifier.
Retour en haut
Résolution de problèmes
À l'aide d'un tableau des nombres
Un motif en croix est un carré plus les quatre carrés directement en haut, en bas, à gauche et à droite de celui-ci.
Un motif en X est un carré plus les quatre carrés qui le touchent en diagonale.
Choisir n'importe quel carré qui ne se trouve pas sur le bord d'un tableau des nombres. Trouver les motifs en croix et en X et additionner leurs sommes. Pouvez-vous expliquer pourquoi ils totalisent le même nombre ? Pouvez-vous trouver les autres motifs qui fonctionnent de cette façon ? Pouvez-vous comprendre comment prédire la somme de motif en croix ou en X pour un nombre quelconque ? (Source : lien #2)
- Commencer avec toutes les cartes à faces visibles sur le tableau des nombres 1-100. Retourner tous les multiples de 2 sauf 2 lui-même. Déplacer au prochain numéro qui est toujours face visible. Retourner tous les multiples de cette valeur sauf la valeur elle-même. Considérer les cartes restantes à faces visibles. Quelles propriétés partagent-elles ? Le numéro 1, appartient-il ?
- Jouer "Deviner le nombre"
- Le nombre est plus grand que 5 x 7.
- Le nombre est plus petit que 120 - 30.
- Le nombre n'est pas un multiple de 10.
- La somme des deux chiffres est 11.
- Je dis ce nombre quand je compte par intervalles de 5.
- Quel est le nombre ?
- Créer votre propre devinette de "Deviner le nombre" (basé sur le lien #5)
À l'aide d'un tableau d'addition
- Utiliser le tableau d'addition pour démontrer que la somme deux nombres impairs est toujours un nombre pair.
Qu'en est-il de la somme de deux nombres pairs ? Quel est le résultat de la somme d'un nombre pair et d'un nombre impair ? Convaincre un ami que ces généralisations sont vraies.
Retour en haut
Fonctionnalités
| Boutons |
Descriptions |
|
Tout retourner
Choisir une des options suivantes :
- montrer les valeurs de toutes les cartes du tableau.
- cacher les valeurs de toutes les cartes du tableau.
- retourner toutes les cartes du tableau.
|
|
Les options pour accéder à différents tableaux
Choisir une des options suivantes :
- les faits d'addition jusqu'à 12 + 12
- les faits de multiplication jusqu'à 12 x 12
- tableau des nombres 0-99
- tableau des nombres 1-100
|
|
Mode de dessin
Dessiner à main levée en cliquant et en faisant glisser.
|
|
Effacer
Effacer des dessins à main levée et des cercles en faisant glisser la gomme sur le tableau des nombres.
|
|
Timbre circulaire
Montrer ou cacher des cercles sur des cartes en :
- cliquant sur des cartes individuelles
- cliquant et en glissant sur plusieurs cartes
|
|
Supprimer
Supprimer toutes les annotations (c'est-à-dire le dessin à main levée et les timbres circulaires).
|
  |
Anglais/Français
Passer de l'anglais au français et vice versa.
|
|
Informations
Ouvrir une boîte de dialogue avec des liens vers cette page de support, un formulaire de rétroaction, ainsi que les informations de droit d'auteur et le numéro de version.
|
|
Retourner
Cliquer pour retourner toutes les cartes de la rangée ou de la colonne correspondante.
|
Retour en haut
Mode d'annotation
Cliquer sur le bouton crayon, gomme ou cercle pour activer le mode d'annotation.
Un masque gris avec une bordure jaune apparaît pour indiquer que l'outil est en mode d'annotation.
Pour quitter le mode d'annotation et reprendre l'interaction avec le tableau des nombres, cliquer sur le
x dans le coin supérieur droit du masque gris. Vous pouvez également cliquer à nouveau sur le bouton en surbrillance pour quitter le mode d'annotation.
Paramètres URL
Les paramètres d'URL permettent d'ouvrir l'outil avec certaines fonctionnalités prédéfinies.
Par exemple, cliquer sur le lien suivant :
https://mathies.ca/tools/NumberChart/index.html?title=Tableau%20des%20nombres&language=fr&show=false&chart=100
L'outil Tableau des nombres va s'ouvrir et afficher la version française du tableau 1-100 avec toutes les cartes à faces cachées.
Noter que la section de paramètre de l'URL commence par un ? (point d'interrogation), et peut inclure n'importe lequel des quatre paramètres facultatifs dans n'importe quel ordre. Le symbole & doit séparer les paramètres.
| Paramètres |
Descriptions |
Valeurs autorisées |
| title |
Définir le texte qui apparaît dans le titre de l'onglet du navigateur.
Valeur par défaut : Tableau%20des%20nombres, où% 20 indique un espace. |
Texte simple |
| langage |
Déterminer le paramètre de langue pour l'outil.
Valeur par défaut : en (English) |
|
| show |
Déterminer si l'outil s'ouvre avec toutes les cartes à faces visibles.
Valeur par défaut : true |
|
| chart |
Déterminer le type de tableau.
Valeur par défaut : mul (tableau des multiplications) |
|
Retour en haut
Liens
- Activity 6 of WINS: Multiplication Facts to 7 x 7 and WINS: Multiplication Facts to 9 x 9
- 30+ Things to Do with a Hundred Chart
- 0-99 or 1-100
- Developing Computational Proficiency with Addition and Subtraction
- Guess the Number
- Mettre l'accent sur les éléments fondamentaux en mathématiques - Guide à l'intention du personnel enseignant
Bandes de fractions
Bloc-notes
Blocs mosaïques géométriques+
L'outil d'ensemble
Monnaie
Réglettes+
Rekenrek
Tableau des nombres
Tuiles algébriques
Tuiles de couleur
