Blocs mosaïques géométriques+

Le contenu

Description

• Les concepts mathématiques
• Établissement des liens entre les concepts fondamentaux en mathématiques et les blocs mosaïques géométriques +

Exemples

• Les conceptions et les dessins
• Le sens du nombre
• Les propriétés géométriques
• La modélisation
• La mesure et la géométrie
  • Les unités de mesure de longueur et de surface des blocs mosaïques géométriques
  • Le périmètre et l'aire
  • Les relations d'aire
  • Les mesures d'angles
  • Les figures similaires
  • La hauteur d'un triangle équilatéral
• Fractions et décimaux
• Algèbre
• Créer un contour de casse-tête

Échantillons de fichiers
Fonctionnalités des outils

• Boutons
• Autres fonctionnalités

Raccourcis clavier
Liens

Description

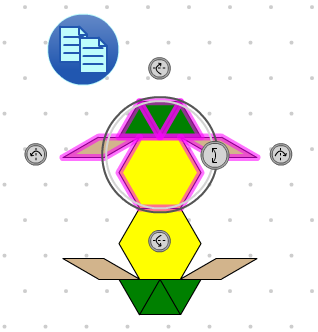
L'outil Blocs mosaïques géométriques+ est un outil de manipulation virtuelle similaire du matériel de manipulation utilisé couramment dans les salles de classe. Dix-huit figures planes différentes peuvent être glissées sur l'espace de travail à partir du panneau de sélection déroulant à gauche. Une fois sur l'espace de travail, elles peuvent être déplacées, copiées, reflétées ou pivotées, individuellement ou par groupes. Les blocs représentant les dixièmes sont inclus. La couleur de chaque type de bloc peut être modifiée. Les élèves peuvent développer de nombreux concepts mathématiques en créant des conceptions et des dessins. L'espace de travail affiche une grille isométrique de petits triangles équilatéraux, ce qui est unique, car plusieurs activités de superficie utilisent un quadrillage carré (voir l'analyse des unités de mesure de longueur et de surface dans la section de la mesure et la géométrie ci-dessous).

Accéder à une grande variété d'outils d'annotations pour communiquer la pensée.
Insérer une image dans l'outil.
Les travaux créés dans un outil mathies peuvent être enregistrés* et ouverts*. Un fichier enregistré peut être partagé avec des pairs ou soumis à un enseignant / une enseignante. Le fichier contiendra toutes les étapes de la solution dès le début jusqu'à la fin.
*Les informations des opérations de fichiers sont seulement disponibles en anglais.

Prendre une capture d'écran pour l'utiliser dans un portfolio, une présentation, une page web, etc.

Retour en haut

Les concepts mathématiques

Les blocs mosaïques peuvent être utilisés pour développer la compréhension de :

• relations géométriques (y compris la composition et la décomposition de figures planes)
• régularités (y compris des motifs répétés, croissants linéaires et des motifs comportant un ou deux attributs)
• mesures de longueurs et de surfaces (y compris le périmètre et d'unités de mesure non conventionnelles)
• propriétés des polygones et des angles (y compris la symétrie)
• transformations (translations, réflexions, rotations et homothétie)
• congruence et similitude
• fractions et décimaux (y compris la représentation, la comparaison, le classement, l'équivalence et les opérations)
• dallages
• variables, expressions et équations

Retour en haut

Établissement des liens entre les concepts fondamentaux en mathématiques et les blocs mosaïques géométriques+

Les compétences et concepts fondamentaux (Lien #1)	Blocs mosaïques géométriques+ et les liens aux concepts fondamentaux
Développer le sens du nombre : comprendre et utiliser les nombres (c.-à-d. pouvoir lire, compter, dénombrer, représenter, ordonner, estimer, comparer, composer, décomposer et recomposer des nombres).	Les blocs mosaïques géométriques+ peuvent être utilisés pour : représenter des fractions et des nombres décimaux à l'aide d'un modèle de surface et d'un modèle d'ensemble identifier les différentes figures planes en tant que le tout et établir un lien entre les autres figures à ce tout (p. ex., quelle fraction du pentagone blanc est l'hexagone double ?) pratiquer à dénombrer les unités fractionnaires ordonner des fractions en considérant l'aire d'une représentation de bloc. composer et décomposer des figures planes et les relier à des mesures et à des opérations numériques (p. ex., un sixième d'un hexagone plus un tiers d'un hexagone est égal à la moitié d'un hexagone) démontrer et expliquer le concept de fractions équivalentes relier les fractions, les nombres décimaux, les pourcentages et les rapports
Reconnaître et utiliser les propriétés des opérations : comprendre les propriétés des opérations afin de développer des stratégies efficaces pour maîtriser les faits mathématiques et effectuer des calculs.	Les blocs mosaïques géométriques+ peuvent être utilisés pour : établir des relations entre l'addition et l'ajout établir des relations entre la soustraction et le retrait établir des relations entre la multiplication et les additions répétées établir des relations entre la multiplication et la fraction "d'un" nombre reconnaître que les propriétés commutatives et associatives s'appliquent à l'addition et à la multiplication de fractions
Maîtriser les faits numériques : comprendre et se rappeler des faits numériques, en ayant recours à des stratégies de rappel variées.	Les blocs mosaïques géométriques+ peuvent être utilisés pour : créer une disposition rectangulaire qui représente un produit de deux nombres naturels appliquer sa connaissance des faits relatifs aux nombres naturels pour aider à reconnaître les régularités lors des opérations sur des fractions pratiquer les faits numériques lors de la résolution de problème relatif à la modélisation et à l'algèbre
Développer les compétences en calcul mental : effectuer mentalement des calculs sans l’aide, ou presque, de papier-crayon et de calculatrices.	L'utilisation d'outils visuels lors de l'apprentissage d'opérations mathématiques permet aux élèves de s’appuyer sur ces modèles et visualisations mentales pour effectuer des calculs mentaux. Les élèves vont développer les compétences en calcul mental à l'aide des blocs mosaïques géométriques+ lorsqu'ils : déterminent l'aire et le périmètre des blocs mosaïques et des figures composées résolvent des problèmes relatifs à l'addition et à la soustraction de fractions et de nombres décimaux multiplient et divisent par 10 et 0,1
Développer le sens des opérations : effectuer des calculs de manière efficiente, avec efficacité et précision et en démontrant une bonne compréhension des faits numériques, des propriétés des opérations et de leur application à la résolution de problèmes.	Les blocs mosaïques géométriques+ peuvent être utilisés pour : reconnaître la relation inverse entre l'addition et la soustraction (p. ex., puisque 1/6 + 1/3 = 1/2, puis 1/2 - 1/6 = 1/3) reconnaître la relation inverse entre la multiplication et la division (p. ex., puisque 1/2 x 6 = 3, puis 3 ÷ 1/2 = 6) expliquer pourquoi la division des nombres positifs par 0,1 donne un résultat plus grand décrire des relations multiplicatives entre des quantités en utilisant des fractions et des nombres décimaux simples démontrer une compréhension sur le raisonnement proportionnel à l'aide des rapports et des taux unitaires

Relier les concepts fondamentaux en mathématiques avec mathies.ca (brouillon)

Retour en haut

Exemples

Les conceptions et les dessins

Les élèves développent leur raisonnement spatial quand ils créent des conceptions ainsi que des dessins et ils les copient ou les modifient.

Certaines activités possibles incluent :

• Créer un dessin d'une fleur à l'aide des blocs mosaïques
  Remarquer : ceci est un exemple de problème dans le domaine de la géométrie et sens de l'espace de la 1^re année tiré du curriculum anglais. L'attente se retrouve sous le titre Relations géométriques : créer des motifs, des images et des conceptions à l'aide des figures planes communes.
  
  
• Créer un hexagone en assemblant des figures planes plus petites.
  Remarquer : ceci est un exemple de problème dans le domaine de la géométrie et sens de l'espace de la 3^e année tiré du curriculum anglais. L'attente se retrouve sous le titre Relations géométriques : résoudre des problèmes en utilisant le moindre nombre ou le plus nombre possible de figures géométriques en deux dimensions (p. ex., mosaïques géométriques) nécessaires pour construire une plus grande figure plane selon divers moyens (p. ex., pour recouvrir un casse-tête).
  
  
• Créer la conception ci-dessous :
  
  
  
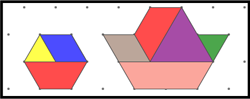
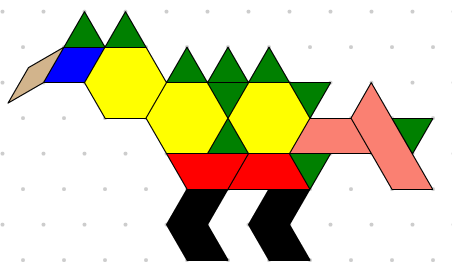
• Avec le modèle de dinosaure ci-dessous, les élèves peuvent :
  • ouvrir l'image grise à partir de l'échantillon de fichier et la recouvrir à l'aide des blocs mosaïques géométriques. On peut demander aux élèves d'utiliser le plus grand nombre et le plus petit nombre de mosaïques géométriques, ou le plus grand nombre de blocs différents.

    Sur un ordinateur de bureau, cliquer sur l'image ci-dessus pour ouvrir ce fichier.

    
    
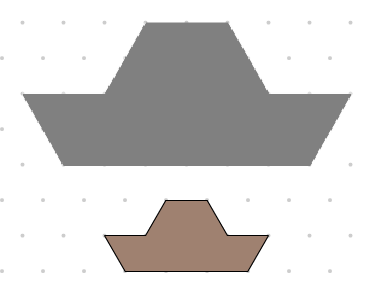
• Avec le modèle de bateau gris ci-dessous, les élèves peuvent :
  • construire la figure en se disant qu'il est similaire au bloc du bateau brun, mais avec des côtés qui sont deux fois plus longs.
    (Les élèves plus âgés peuvent tirer des conclusions sur les angles à partir d'une comparaison de ces deux figures similaires.)
  • ouvrir l'image grise à partir de l'échantillon de fichier et la recouvrir à l'aide des blocs mosaïques géométriques.
    Les élèves peuvent appliquer différentes règles (p. ex., les blocs de recouvrement peuvent surpasser l'image, les blocs de recouvrement peuvent se chevaucher, les espaces ne sont pas permis).
    

    Sur un ordinateur de bureau, cliquer sur l'image ci-dessus pour ouvrir ce fichier.

  • ouvrir un fichier auquel des questions ont été ajoutées par leur enseignant/enseignante.
    
  • placer un bloc brun à divers endroits et trouver le centre de l'hométhétie qui produirait l'image grise.
    
  • créer leur propre contour gris d'un casse-tête et demander à leurs camarades de le recouvrir de diverses façons (voir les instructions).
  
  
• Rechercher sur le Web pour des motifs de carrelage qui peuvent être construits à l'aide des blocs mosaïques géométriques+. L'article anglais de Wikipédia sur les pavages par des polygones est un bon point de départ. Décrire le motif et les transformations qui sont nécessaires pour prolonger le modèle. Identifier les symétries qui en résultent (voir trois exemples additionnels qui se trouvent ci-dessous dans la section des propriétés géométriques).
  

Retour en haut

Le sens du nombre

De nombreuses activités de dénombrement WINS incorporent l'utilisation des blocs mosaïques géométriques+ (cliquer liste d'activités pour étendre la liste).

Dénombrer le nombre de différents types de blocs dans une conception.

Composer et décomposer des nombres naturels
Visiter les activités WINS pour composer et décomposer des nombres. Ces activités y comprises, Le regroupement et la décomposition des nombres naturels jusqu'à 5, Le regroupement et la décomposition des nombres naturels jusqu'à 10 et Le regroupement et la décomposition des nombres naturels jusqu'à 20.



Comparer et ordonner des nombres naturels
Visiter les activités WINS pour comparer et ordonner des nombres. Ces activités y comprises, Comparer et ordonner des nombres naturels jusqu'à 10 et Comparer et ordonner des nombres naturels jusqu'à 20.


Retour en haut

Les propriétés géométriques

Classer une collection de figures selon leurs propriétés géométriques.
(p. ex., le nombre des côtés, la longueur des côtés, le nombre d'angles intérieurs, le nombre d'angles droits, l'aire, le périmètre, les axes de symétrie).

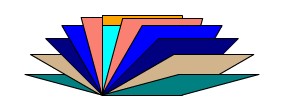
On pourrait demander aux élèves comment le tri ci-dessus a été organisé.


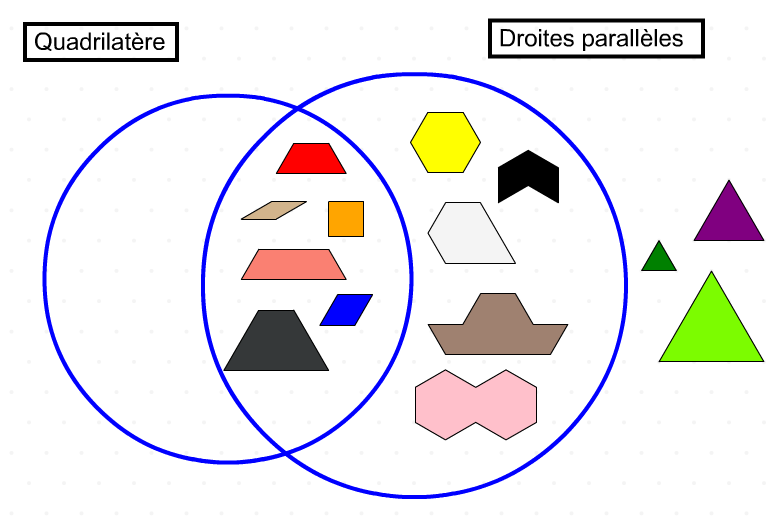
À l'aide du diagramme de Venn au-dessus, cette classification soulève des questions intéressantes.

• Est-il possible qu'un quadrilatère ne possède pas des côtés parallèles ? Si c'est le cas, utiliser la fonction d'annotation pour en dessiner un.
• Quelles autres classifications générales des figures géométriques ne sont pas représentées par un bloc mosaïque (p. ex., des triangles isocèles) ?
  Concevoir de nouveaux blocs pour représenter certaines de ces figures (p. ex., un triangle isocèle avec deux angles de 45°).

Des défis.

1. Est-il possible de créer un quadrilatère sans côtés parallèles composés de blocs mosaïques géométriques ?
   
   L'utilisation des angles intérieurs des blocs mosaïques géométriques peut aider.
   La réponse, dépend-elle du fait que les blocs peuvent se chevaucher ou s'aligner à la grille ?
      
2. Concevoir un bloc mosaïque quadrilatère sans droites parallèles.
   
   Utiliser du papier isométrique triangulaire (voir Dynamic Paper de NCTM), un logiciel de géométrie dynamique ou un logiciel de conception à 2D, si disponible.
   
   Une solution possible : Geometer's Sketchpad a été utilisé pour créer un bloc mosaïque quadrilatéral de couleur prune.
   
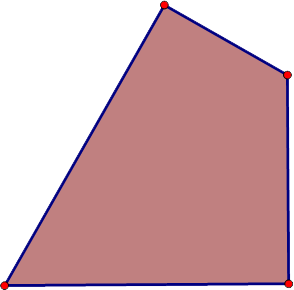
   La conception ci-dessous, à été créée par les étapes suivantes.
   
   1. L'inserstion d'une image du bloc quadrilatéral de couleur prune dans l'outil Blocs mosaïques géométriques+.
   2. En faisant glisser le bloc mosaïque du trapèze rouge sur l'espace de travail; en pivotant et en redimensionnant l'image du bloc de couleur prune pour qu'elle corresponde à la longueur d'un côté du trapèze rouge.
   3. En copiant l'image du bloc de couleur prune et la positionner à côté de l'image originale.
   4. En faisant glisser et positionner les autres blocs mosaïques.
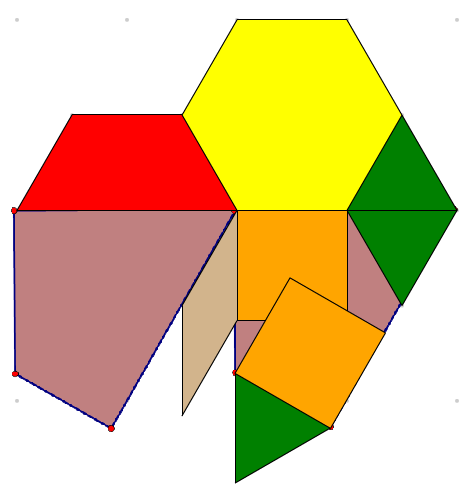
   Remarquer : les deux blocs carrés oranges et le bloc triangulaire vert sont placés sur l’image de bloc de la couleur prune. Désactiver le magnétisme à la grille afin de placer ces blocs dans les coins du bloc de couleur prune. Ces blocs nous aident à voir les angles à 90°, 60°, 90° dans trois des coins du bloc de couleur prune. Quelle est la mesure du quatrième angle ?
   

Créer et identifier les figures planes congruentes.
Les figures planes congruentes sont créées en les copiant, par la translation, la réflexion et la rotation à l'aide de l'outil Blocs mosaïques géométriques+.

Les élèves peuvent également être invités à :

• créer chaque conception à l'aide des Blocs mosaïques géométriques+
• décrire certaines des transformations observées dans la conception
• trouver le motif et des transformations à plusieurs reprises pour créer la conception

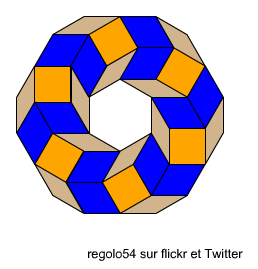
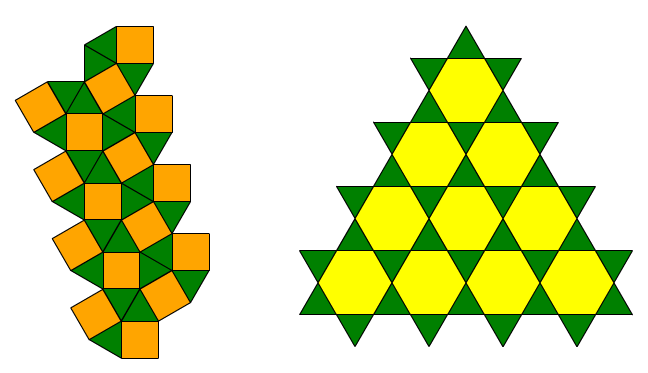Remarquer : la première figure ci-dessus est accessible en tant qu' échantillon de fichier. Utiliser les boutons annuler et rétablir pour voir une façon dont la séquence des étapes prises identifie le motif et applique la transformation.

Deviner ma figure.
Les élèves travaillent en partenaires. Chaque élève crée une figure à l'aide des blocs mosaïques géométriques, cachés de la vue de son partenaire. À tour de rôle, les élèves fournissent des indices décrivant leur figure à l'aide de la terminologie mathématique appropriée. Sur la base de cet indice, le partenaire tente de reproduire la figure. Les élèves continuent à échanger des indices jusqu'à ce que chaque partenaire puisse reproduire la figure de l'autre.

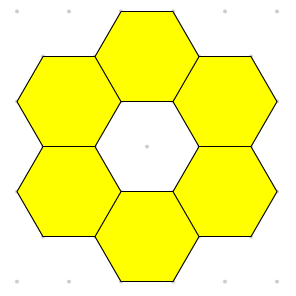
Quelques exemples d’indices pour la figure ci-dessus.

• La figure est composée de six blocs.
• Chaque bloc partage un côté avec exactement deux autres blocs.
• Les six blocs sont congruents.
• Il y a plus de 4 lignes de symétrie.

Quel est le périmètre de cette figure ? (Cette question pourrait susciter un discours mathématique animé!)

Retour en haut

La modélisation

Identifier, prolonger et créer des motifs répétés.

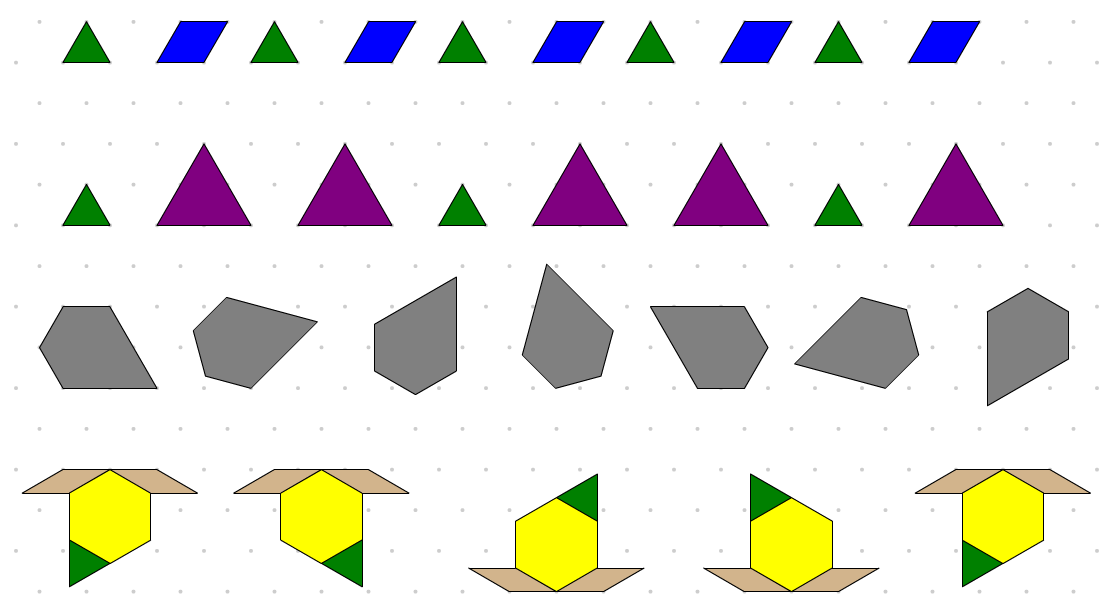
Les élèves démontrent qu'ils comprennent que les modèles résultent de l'utilisation d'une transformation (p. ex., translation, réflexion, rotation), ou d'un autre changement répété d'un attribut (p. ex., figure, taille, couleur, orientation, nombre).
Remarquer : en ce qui concerne les mosaïques géométriques, tous les blocs ayant une figure donnée ont la même couleur, ce qui limite le nombre d'attributs qui peuvent changer. Pour créer des motifs avec plus d'attributs, envisager d'utiliser l'outil d'ensemble.

Les élèves peuvent prolonger et créer des motifs répétés à partir des transformations de réflexion et rotations.

Créer un train à l'aide des blocs mosaïques géométriques en alternant un triangle vert avec un trapèze rouge. Prédire quel bloc sera au 30^e rang.
Remarquer : ceci est un exemple de problème dans le domaine de la modélisation et algèbre de la 4^e année du curriculum anglais. L'attente se retrouve sous le titre Relations : déterminer la régularité relative aux suites non numériques et numériques des motifs répétés.

Identifier, prolonger et créer des motifs croissants.

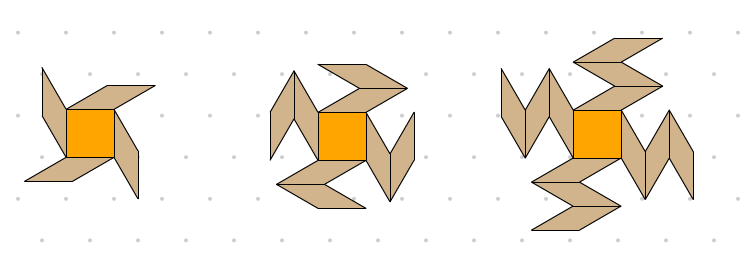
L'image ci-contre démontre les 3 premières figures d'une suite non numérique à motif croissant linéaire.
À quoi ressemblera l'image de la 10^e figure ?
Combien de blocs y aura-t-il au cours de la 10^e figure ?
Combien de blocs y aura-t-il au cours de la 100^e figure ?
Existe-t-il une figure qui contient 45 blocs ? 300 blocs ?

Les élèves créent des représentations visuelles des suites non numériques à motif croissance linéaire, puis posent et répondent à des questions relatives aux régularités.

Retour en haut

La mesure et la géométrie

Le curriculum de l'Ontario anglais (Lien #2) suggère d'utiliser des blocs mosaïques comme des unités de mesure non conventionnelles de longueur, d'aire et de volume.

Les activités qui exigent de recouvrir les conceptions et les dessins (voir ci-dessus) répondent également à divers attentes en matière de géométrie que l'on retrouve dans le curriculum de l'Ontario.

Les élèves prennent des mesures de figures composées et les relient aux longueurs des côtés, aux superficies et aux angles des blocs mosaïques géométriques de base.

Les unités de mesure de longueur et de surface des blocs mosaïques géométriques.

L'outil Blocs mosaïques géométriques+ utilise une grille isométrique triangulaire.
Une unité de longueur typique est une distance entre les points adjacents, qui est une longueur de côté de six premiers blocs mosaïques usuels.
Une unité de mesure de surface typique est l'aire du petit triangle vert.

Lorsqu'on utilise un quadrillage de 1 cm sur 1 cm, les longueurs sont généralement mesurées en centimètres et les surfaces en centimètres carrés.

Sur la grille de Blocs mosaïques géométriques+, la surface du petit triangle vert n'est pas le carré de la longueur de ses côtés. C'est le bloc orange qui a une aire égale au carré de sa longueur de côté.

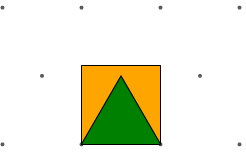
L'aire du carré est deux fois plus que l'aire du triangle.
Indice : tracer une ligne verticale au milieu de la figure plane. Plus précisément, la surface du petit triangle vert représente environ 43% de la surface du carré orange.

L'aire de l'hexagone jaune - Deux approches
Lorsque nous disons que l'aire de l'hexagone jaune est 6, nous entendons que cela veut dire que c'est la même que l'aire de 6 petits triangles verts.

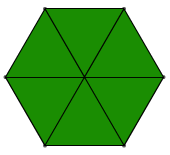
Cependant, l'aire de l'hexagone jaune comparé au mesure de l'aire des carrés oranges, est inférieure à 4, comme illustré par l'image ci-dessous.

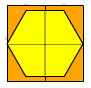
La surface de l'hexagone jaune est en réalité inférieure à 3 carrés oranges.

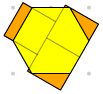Indice : comparer l'aire de l'hexagone qui n'est pas au-dessus des carrés à l'aire des carrés qui ne sont pas sous l'hexagone.

Lors de la mesure, il est très important de bien définir les unités utilisées. En faisant la comparaison, si le petit triangle vert mesure une unité, cela veut dire que l'hexagone jaune mesure 6 unités. Cependant, l'hexagone jaune mesure environ 2,6 unités carrées lorsqu'on utilise un quadrillage carré.

Retour en haut

Exemple 1 - Le plus grand périmètre pour une aire conservée

Créer une figure composée à l'aide de six blocs hexagones jaunes avec un périmètre le plus grand possible.
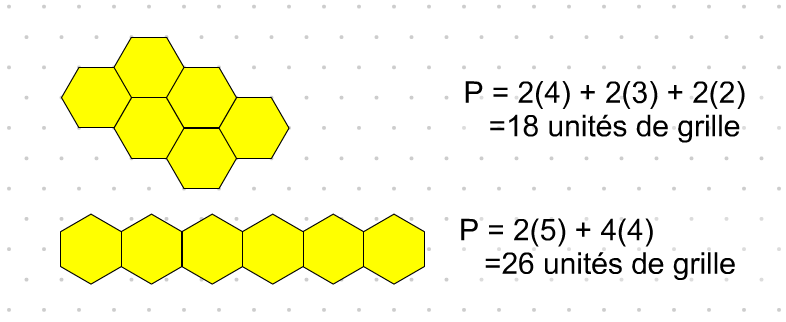
Encourager les élèves à utiliser des stratégies de calcul efficaces pour calculer les périmètres.

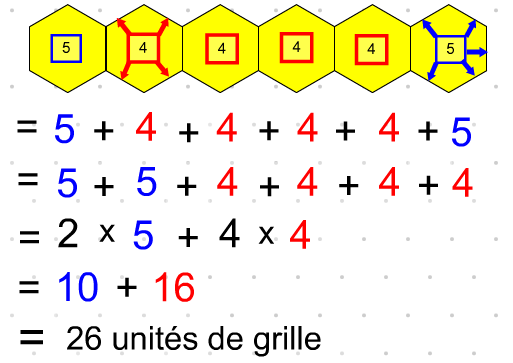
Extensions :

• Modifier le nombre de blocs permis pour créer une figure composée.
• Modifier le type de blocs permis pour créer une figure composée.
• Créer des figures composées avec la plus grande surface possible pour un périmètre donné.
• Identifier les angles de 60°, 120°, 240°, et 360° à partir des figures composées créées.

Retour en haut

Exemple 2 - Relier l'aire d'un triangle, d'un parallélogramme et d'un rectangle

Relier l'aire d'un triangle à un parallélogramme.

Un raisonnement inductif pour laquelle le parallélogramme (dans ce cas un losange) a deux fois l'aire du grand bloc triangulaire vert :

• reconnaître que le parallélogramme est composé de deux grands blocs triangulaires verts congruents
• compter le nombre de petits blocs verts dans chacun des grands blocs triangularires verts (9 et 18)

Relier l'aire d'un triangle à un rectangle.

• Utiliser la fonction d'annotation pour dessiner un rectangle bleu autour du triangle vert pâle. Dessiner des triangles de couleurs dans l'espace blanc. Faire pivoter les triangles dessinés pour recouvrir le triangle vert pâle.
• Raisonner que le rectangle a une aire deux fois plus grande que le triangle vert pâle.

Relier l'aire d'un parallélogramme à un rectangle.

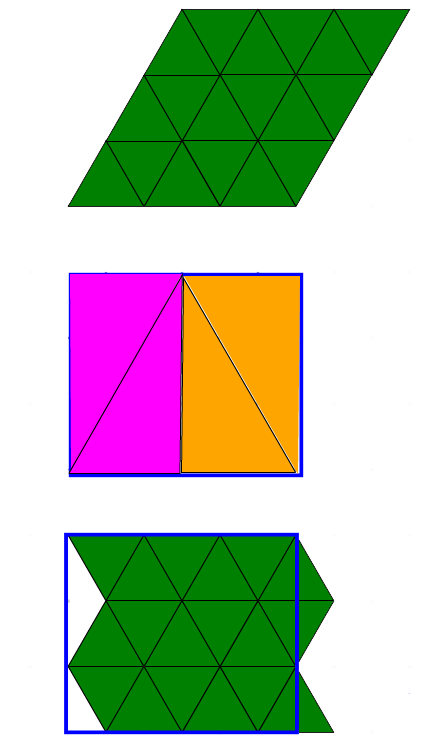
• Raisonner que l'aire du parallélogramme est la même que celle du rectangle puisqu'ils sont deux fois le triangle vert pâle.
• Utiliser les petits blocs verts pour vérifier que le nombre de blocs requis pour recouvrir le parallélogramme couvrira également le rectangle.

Les blocs mosaïques sont utilisés pour de nombreuses activités. L'activité comme celle de ci-dessus vise à introduire le concept d'aire et à donner des expériences viscérales aux élèves, relatives aux relations de surface qui peuvent être étendues à des cas plus généraux.

Retour en haut

Exemple 3 - Les mesures d'angles

Déterminer les angles intérieurs et extérieurs de tous les blocs mosaïques géométriques en les reliant aux angles intérieurs du triangle équilatéral de 60°.
Par exemple, déduire que les angles dans le losange beige sont de 30° et 150°.


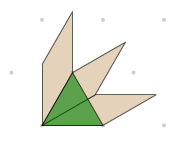Vérifier les propriétés incluant :

• un angle plat est 180°
• les angles dans un triangle totalisent à 180°
• les angles dans un quadrilatère totalisent à 360°
• un angle extérieur d'un triangle est égal à la somme des deux angles intérieurs opposés

Retour en haut

Exemple 4 - Les figures similaires

Relier les aires et les périmètres de figures similaires.
Par exemple :

• Le bateau gris a un périmètre de deux fois plus grand que le bloc mosaïque du bateau brun et a quatre fois sa superficie.
  
• Le grand bloc mosaïque vert pâle a un périmètre qui est trois fois plus grand que le petit bloc vert foncé et a neuf fois sa superficie.
  

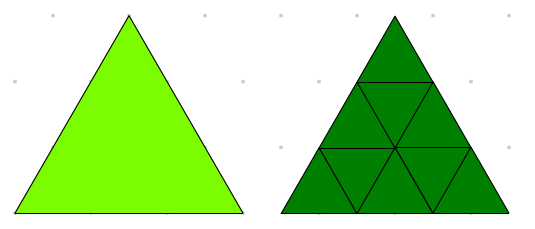
Retour en haut

Exemple 5 - La hauteur d'un triangle équilatéral

Remarquer : lorsqu'un côté d'un triangle est identifié comme la base,

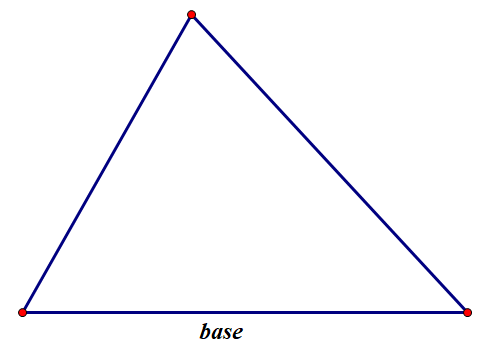
le segment perpendiculaire à la base à partir du sommet opposé est appelé la hauteur ou l'altitude d'un triangle.

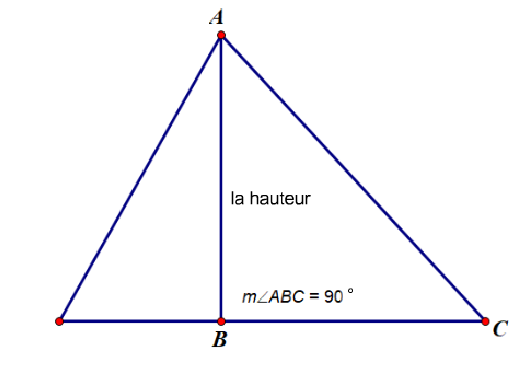
En 7^e année, les élèves apprendront que, quel que soit le côté considéré comme la base, l'aire est égale à la moitié de la longueur de la base multipliée par la hauteur à partir de cette base.

Relier la hauteur du bloc de triangle vert à sa longueur de côté.


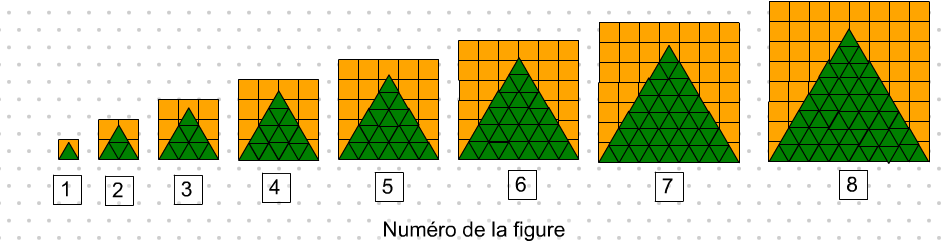Cliquer sur l'image ci-contre pour la voir en taille réelle, sans distorsion.

Pour chaque numéro de la figure ci-dessus, raisonner que la hauteur est :

1. moins que sa longueur de côté
2. plus de la moitié de sa longueur de côté
3. plus des deux tiers de sa longueur de côté
4. plus des trois quarts de sa longueur de côté
5. plus de quatre cinquièmes de sa longueur de côté
6. plus de cinq sixièmes de son côté
7. très proche de six septièmes de sa longueur de côté
8. moins de sept huitièmes de son côté

Utiliser le théorème de Pythagore pour relier la hauteur du bloc triangulaire vert à sa longueur de côté.
La différence entre l'estimation des six septièmes et la valeur réelle est inférieure à 1%.

Créer diverses suites numériques à partir de la séquence ci-dessus.

• nombre des carrés
• nombre des triangles
• nombre des blocs mosaïques géométriques

Résoudre les problèmes connexes (p. ex., quel est le prochain terme, le 20^e terme, le terme général ?).

Des faits intéressants sur les triangles
(qui ont très peu à voir avec les blocs mosaïques géométriques)

Les trois altitudes d'un triangle sont concourantes. Leur point d'intersection est appelé l'orthocentre du triangle. Ce point est le centre d'un cercle qui peut être construit en créant un triangle anticomplémentaire dont les côtés sont parallèles au triangle d'origine par ses sommets (voir ci-dessous).

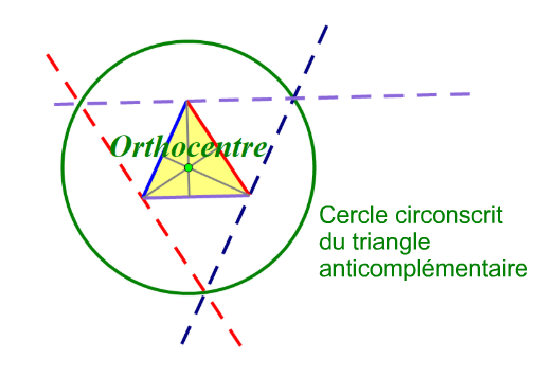
Autres "centres" d'un triangle incluent le centre du cercle circonscrit, le centre du cercle inscrit, et le centre de gravité (ou barycentre), bien que pour un triangle équilatéral, ils soient tous les mêmes.

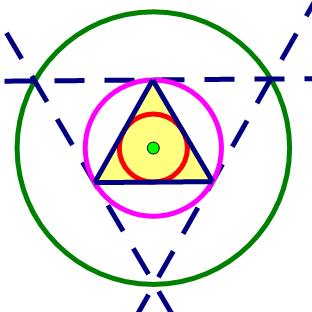
Le dessin ci-contre illustre un triangle équilatéral jaune avec un cercle inscrit rouge, un cercle circonscrit violet et un cercle circonconscrit vert du triangle anticomplémentaire.

Accéder à des informations supplémentaires : "LES DROITES REMARQUABLES et les points particuliers dans un triangle".

Retour en haut

Fractions et décimaux

Quelle fraction de cette figure a une surface verte ?

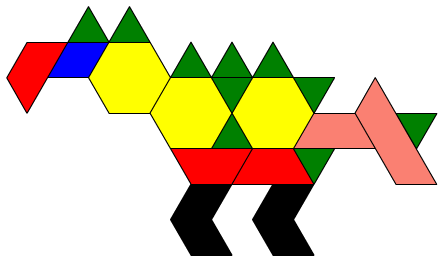
Les élèves peuvent utiliser un modèle de surface pour déterminer la fraction.

Les élèves peuvent :

• identifier le triangle vert comme une pièce unitaire qui pourrait être utilisée pour recouvrir la figure entière,
• dénombrer le nombre de triangles verts nécessaires pour recouvrir toute la figure (55),
• nommer un triangle vert en fraction unitaire (1/55),
• déterminer l'aire de la surface verte en dénombrant en fraction unitaire (p. ex., 1/55, 2/55, 3/55, … 10/55), et
• reconnaître que le dénombrement des triangles verts donne la fraction correcte (10/55 de la figure sont vertes).

On peut également demander aux élèves :

• pour déterminer si l'aire de la surface jaune est supérieure à l'aire de la surface verte.
• quelle fraction des blocs mosaïques est vertes ? (un modèle d'ensemble)
• pour créer une figure qui est cinq sixièmes verts.

Remarquer : cette figure a été créée en utilisant l'échantillon de fichier du dinosaure et en remplaçant le losange beige par un trapèze rouge afin que la surface puisse être exprimée sous forme de triangles verts.

Nommer les fractions

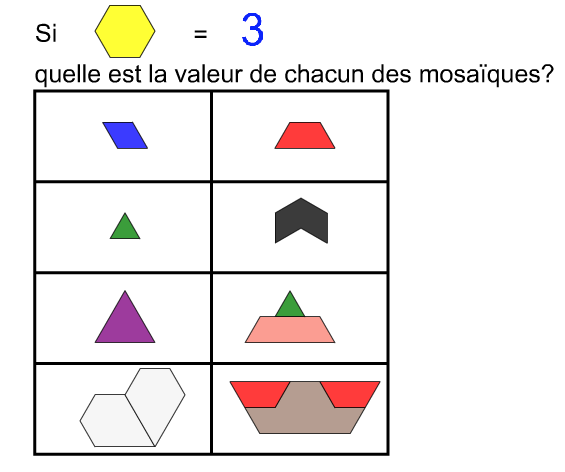
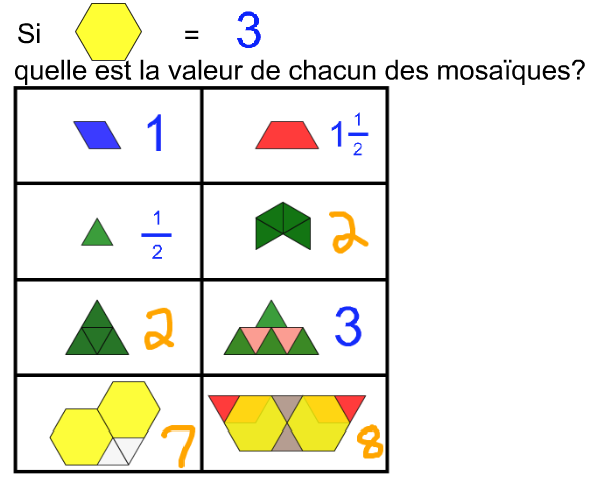
Sur un ordinateur de bureau, cliquer l'image ci-dessus pour ovrir ce fichier.	Clé de réponses

Bien que les élèves puissent utiliser les réglettes pour comparer différentes longueurs, ils peuvent utiliser les blocs mosaïques géométriques et leurs valeurs fractionnaires pour comparer l'aire de diverses figures.

Cet exemple peut être modifié.

• Échanger l'hexagone pour une différente figure plane ou d'une figure composée.
• Échanger le "3" avec l'une des autres images dans le fichier Zip créé à cet effet ou avec toute fraction dessinée à main levée.
• Utiliser différentes figures du tableau.

Les élèves peuvent se lancer des défis : "J'ai deux figures. L'aire d'une figure est d'un huitième et celle de l'autre figure est de trois quarts. Quelles pourraient être mes deux figures ?"
Ou, utiliser un cinquième et trois quarts pour un vrai défi.


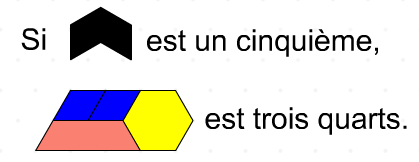
Reporter vous aux activités Changing Wholes with Pattern Blocks* tiré du Parcours d'apprentissage : Les Fractions.

Les nombres décimaux
Les blocs mosaïques géométriques+ peuvent être utilisés pour représenter des nombres décimaux.


Représenter 1,8 de plusieurs façons



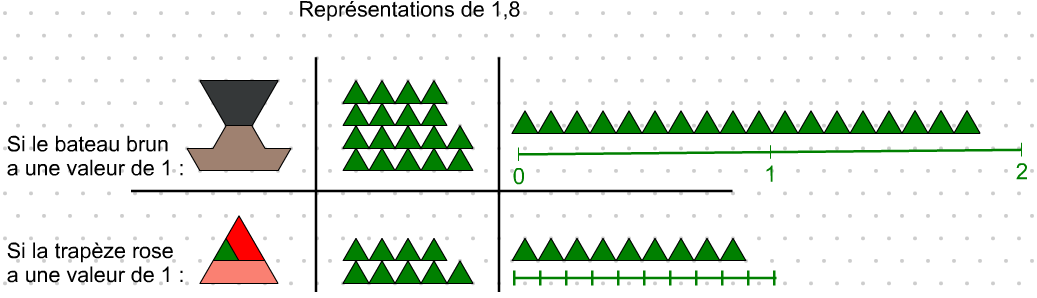Représenter et calculer 0,5 ÷ 0,1



Retour en haut

Algèbre

Créer des expressions et résoudre des équations.
Pour une collection de triangles, le nombre total de côtés est égal à trois fois le nombre de triangles ou c = 3n.
Remarquer : ceci est un exemple tiré du curriculum anglais de la 8^e dans le domaine de la modélisation et algèbre. L'attente spécifique se retrouve sous le titre Variables, expressions et équations : expliquer la règle des relations mathématiques par des énoncés simples en expressions algébriques et en équations.

Résolution de problèmes liés aux règles algébriques.
L'industrie BMG fabrique des tables en forme de bateau. Écrire une expression pour le nombre de sièges. Utiliser s, pour représenter la valeur inconnue des sièges et t, pour représenter le nombre de tables. Combien de tables faut-il pour accueillir 100 personnes ?

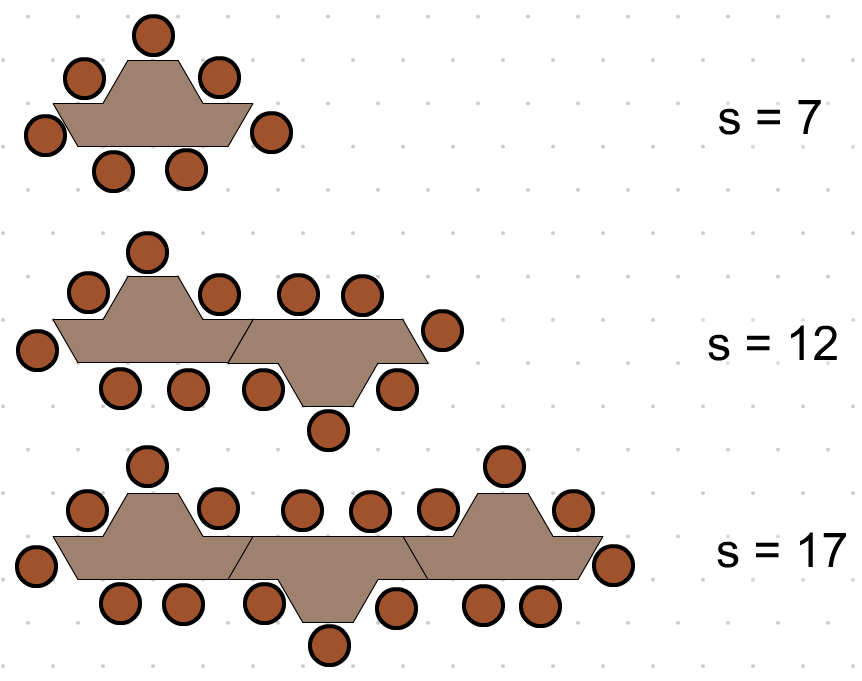Attribuer des valeurs aux divers blocs. Évaluer des expressions algébriques et substituer ces valeurs dans ces expressions. Résoudre les équations simples.
L'industrie BMG fabrique des blocs mosaïques à partir des matériaux misent au rebut.
Il détermine que le coût de production d'un bloc-modèle est de 0,05 $ par coupe.
Ordonner les blocs du moins chers aux plus chers.

L'ordre des premiers quatorze blocs mosaïques ci-dessous suppose qu'une coupe est effectuée pour chaque côté du bloc.

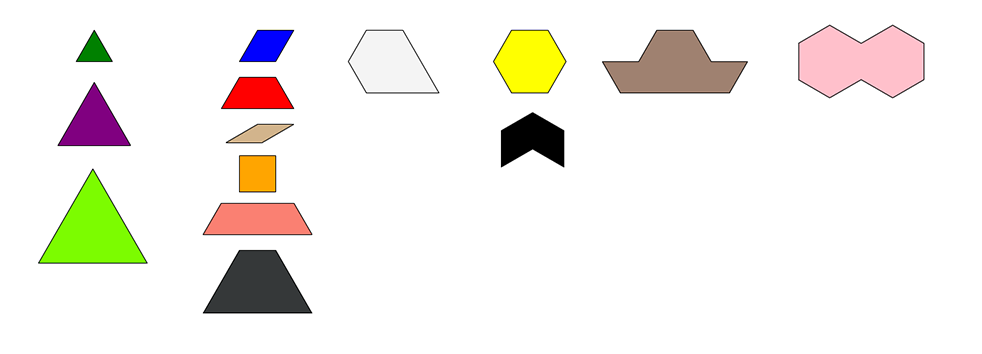
Un entrepreneur décide de daller un sol avec des blocs de l'industrie BMG.
Si l’entrepreneur se soucie uniquement de la couverture au prix le plus bas, quels blocs devrait-il utiliser le plus ?

Un élève peut penser qu'un bloc de chaque groupe ayant la plus grande surface serait le plus rentable, donc il trie ces blocs de la plus rentable à la moins rentable.

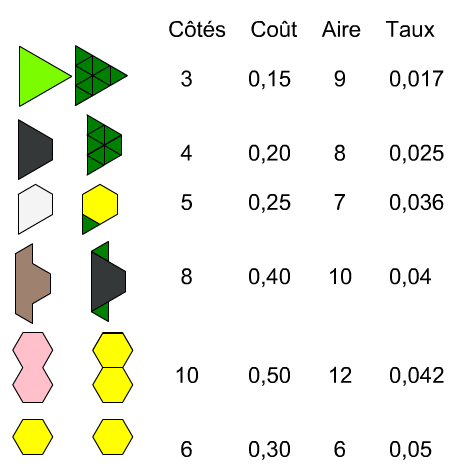
Pour comparer la rentabilité de ces six blocs, on fait un calcul de taux. Que signifie le taux de 0,05 pour l’hexagone ?

Extensions :

• Écrire la relation entre le coût et le nombre de coupes sous forme de fonction linéaire. Créer un graphique de cette fonction. Créer une figure composée qui coûterait 1 $.
• Déterminer comment la situation changerait si le matériau coûtait 0,12 dollar par centimètre carré et que le plus petit bloc est un triangle équilatéral d’une longueur de côté de 1 cm.
• Comparer les coûts de différents types de carrelage pour une pièce de 5 m sur 3 m.

Retour en haut

Créer un contour de casse-tête

Créer un contour de casse-tête, ou modèle, similaire à l'exemple du bateau gris ci-dessus, puis mettre les autres au défi de le recouvrir avec des blocs mosaïques (voir les connexions du curriculum de la l^ère année (disponible en anglais) [Lien #2]).

Le document Créer un contour de casse-tête à l'aide des blocs mosaïques géométriques+ (PDF) décrit comment transformer

une conception de bloc comme en modèle d'un contour de casse-tête comme .

Retour en haut

Échantillons de fichiers

Pour accéder à un échantillon de fichier :

• cliquer sur le lien dans la colonne Échantillons (pour les ordinateurs de bureau uniquement), ou
• utiliser le bouton Ouvrir WWW dans la boîte de dialogue Paramètres et indiquer l'URL, ou
• télécharger le fichier à partir de la colonne URL (cliquer avec le bouton droit de la souris et enregistrer localement sur un ordinateur de bureau ou, sur un appareil mobile, appuyer avec de la force) et utiliser le bouton Ouvrir dans l'outil, ou
• ajouter les échantillons de fichiers mathies du dossier Google Disque (Google Drive) à "Mon disque" (My Drive), ce qui permet un accès pratique à tous les appareils.

Voir la page Opérations de fichiers* (disponible en anglais seulement) pour plus de détails.

Échantillons Cliquer pour ouvrir l'outil - ordinateur de bureau uniquement	URL Taper ou copier dans la zone de texte Ouvrir WWW, ou enregistrer localement en cliquant avec le bouton droit de la souris ou en appuyant fort.
Une conception	https://mathies.ca/files/examples/PB_Ex1.xml
Nommer les fractions Nommer les fractions - Suite Nommer les fractions - Combiner (pour les écrans plus grands) Cette activité regroupe les deux tableaux ci-dessus dans un seul fichier.	https://mathies.ca/files/examples/PB_Ex2fr.xml https://mathies.ca/files/examples/PB_Ex2fr_Suite.xml https://mathies.ca/files/examples/PB_Ex2fr_Combiner.xml
Bateau gris	https://mathies.ca/files/examples/PB_BateauGris.xml
Dinosaure	https://mathies.ca/files/examples/PB_Dinosaure.xml
Modèle de dinosaure	https://mathies.ca/files/examples/PB_ModeleDeDinosaure.xml
Transformation répétée	https://mathies.ca/files/examples/PB_Ex3fr.xml
Conception symétrique 1 Inspiré d'un tweet de @Trianglemancsd et créé par @davidpetro314.	https://mathies.ca/files/examples/PB_Ex4.xml
Conception symétrique 2 Merci à David Petro. Remarquer : ce fichier ne fonctionnera que dans la version 1.0.3 ou une version ultérieure puisqu'il inclut trois nouvelles figure de losanges ajoutées.	https://mathies.ca/files/examples/PB_Ex5.xml

Remarquer : ces fichiers ont été conçus sur un ordinateur de bureau. Il y a la possibilité que les fichiers ne s'ouvriront pas exactement comme indiqués sur les autres appareils.

Retour en haut

Fonctionnalités des outils

Boutons	Descriptions
	La taille des blocs mosaïques géométriques Diminuer / Augmenter la taille des blocs mosaïques géométriques.
	Magnétisme Les blocs mosaïques géométriques s'enclenchent les uns dans les autres et sur la grille isométrique, à moins que ce paramètre ne soit désactivé. Lorsque ce paramètre est activé, les figures peuvent être pivotées à des multiples de 15°.
	Anglais/Français Passer de l'anglais au français et vice-versa.
	Outil d’annotation Cacher / Montrer une grande variété d'outils d'annotation qui peuvent être utilisés pour communiquer la pensée.
	Insérer une image Insérer des images dans l'outil. Plus de détails.
	Annuler/Rétablir Reculer ou avancer dans les actions avec l’outil. Cette fonctionnalité est non seulement utile pour revenir en arrière quand un faux pas est fait, mais permet également aux étudiants et étudiantes de démontrer leur travail dès le début jusqu'à la fin. Les élèves peuvent appuyer sur Annuler jusqu’à ce qu’ils soient au début de leur solution, puis appuyer sur Rétablir à plusieurs reprises pour expliquer chaque étape. Remarquer : Annuler/Rétablir n'est pas disponible pour les objets d'annotation.
	Réinitialiser Ramener l’outil à son état de départ.
	Informations Accéder à un lien vers une page de support, un formulaire de rétroaction, ainsi que les informations de droit d’auteur et le numéro de version.
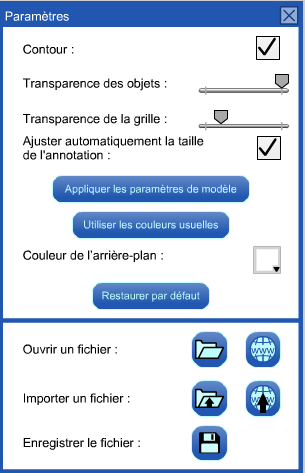
	Paramètres Afficher la boîte de dialogue Paramètres. Le paramètre d'ajuster automatiquement la taille de l'annotation est sélectionné par défaut. Cela signifie que si la taille du bloc mosaïque est modifiée, toute annotation sur l'espace de travail sera mise à l'échelle pour correspondre. Le bouton Appliquer les paramètres de modèle permet de transformer les figures composées en une figure grise sans contour visible. Voir Créer un contour d'un casse-tête pour plus de détails. Le bouton Utiliser les couleurs usuelles est utilisé pour restaurer les couleurs des blocs mosaïques par défaut. Utiliser le bouton Restaurer par défaut pour restaurer tous les paramètres, y compris la couleur des blocs. Ouvrir, importer et enregistrer des fichiers (voir Opérations de fichiers* pour plus de détails disponibles en anglais seulement).
	Supprimer (tout sur l'espace de travail) Cliquer pour supprimer les blocs mosaïques sélectionnés. Si rien n'est sélectionné, tout l'espace de travail sera effacé. Vous pouvez également faire glisser des éléments vers le bac à recyclage pour les supprimer.
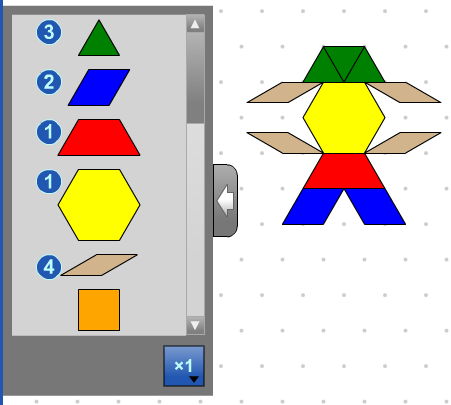
	Comptage de blocs Afficher/Cacher le nombre de blocs utilisés sur l'espace de travail à côté de chaque bloc de clonage. Défiler pour voir tous les blocs mosaïques et leurs comptes.
	Nombre de copies à faire glisser Définir le nombre de copies à faire glisser à partir du panneau de sélection.
	Copier Faire une copie des objets sélectionnés.

Retour en haut

Autres fonctionnalités

Sélection multiple Pour sélectionner des blocs mosaïques, cliquer et faire glisser le curseur pour créer un rectangle de sélection autour d'eux. Pour ajouter à la sélection précédente, créer un rectangle de sélection en maintenant la touche Maj enfoncée. Cliquer sur un bloc mosaïque pour l'ajouter ou le supprimer de la sélection. Les blocs mosaïques géométriques sélectionnés peuvent être déplacés, copiés, pivotés, réfléchies verticalement ou horizontalement, ou supprimés en tant que groupe.

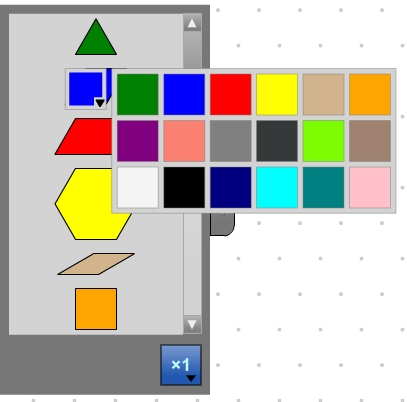
Configurer le panneau de sélection Cliquer sur un bloc de clonage dans le panneau de sélection pour modifier la couleur de tous les blocs de ce type.

Retour en haut

Raccourcis clavier

Les raccourcis clavier usuels ont été mis en oeuvre pour la version de l'outil des ordinateurs de bureau.

Liens

Supports PDF

1. Mettre l'accent sur les éléments fondamentaux en mathématiques - Guide à l'intention du personnel enseignant
2. Relier les concepts fondamentaux en mathématiques avec mathies.ca (Brouillon)
   
3. Créer un contour de casse-tête à l'aide des blocs mosaïques géométriques+
4. Modèle des blocs mosaïques géométriques

Supports PDF anglais

Supports supplémentaires disponibles en anglais


Retour en haut