Description
Examples
Sample Files
Features of the Tool
Keyboard Shortcuts
Links
Description
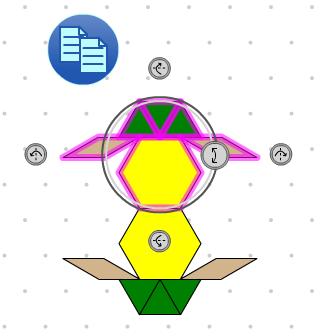
The Pattern Blocks+ Tool is a virtual manipulative similar to the physical ones commonly available in classrooms. Eighteen different shapes can be dragged into the workspace from the scrollable selection panel at the left. Once in the workspace they can be moved, copied, reflected, or rotated, individually or in groups. Blocks to represent tenths are included. The colour of each type of block can be changed. Students can make designs and develop numerous
mathematical concepts. The Pattern Blocks+ workspace shows an isometric grid of small equilateral triangles, which is unique when so many area activities use a square grid (see the discussion of
length and area units in the
Measurement and Geometry section below).
Access a wide variety of
Annotation tools 
to communicate thinking.
Insert pictures
into the tool.
Work created in a mathies tool can be
saved
and
opened
.
A saved file can be shared with peers or submitted to a teacher. The file will contain all solution steps from start to finish.
Take a
screenshot to use as part of a portfolio, presentation, web page, etc.
top
Mathematical Concepts
Pattern Blocks can be used to develop understanding of:
- geometric relationships (including composing and decomposing shapes)
- patterns (including repeating patterns, linear growing patterns and patterns involving 1 or 2 attributes)
- measurement of lengths and areas (including perimeter, and the use of non-standard units)
- properties of polygons and angles (including symmetry)
- transformations (translations, reflections, rotations and dilatations)
- congruence and similarity
- fractions and decimals (including representing, comparing, ordering, equivalence, and operations)
- tessellations
- variables, expressions and equations
top
Connecting Fundamental Math Concepts with Pattern Blocks+
| Fundamental Concepts and Skills (Link #1) |
Pattern Blocks+ Connections |
Working with numbers:
Understanding and using numbers (e.g., being able to read, represent, count, order, estimate, compare, compose, decompose, and recompose numbers).
|
Pattern Blocks+ can be used to:
- represent fractions and decimals using area and set models
- identify different shapes as the whole and relate other shapes to that whole (e.g., what fraction of the white pentagon is the double hexagon?)
- practise counting fractional units
- order fractions by considering the area of a block representation
- compose and decompose shapes and relate to numerical measurements and operations (e.g., one-sixth of a hexagon plus one-third of a hexagon is equal to one-half of a hexagon)
- demonstrate and explain the concept of equivalent fractions
- relate fractions, decimals, percents and ratios
|
Recognizing and applying understanding of number properties:
Understanding how numbers behave in operations and drawing on that understanding to master math facts and perform calculations. |
Pattern Blocks+ can be used to:
- relate addition to combining
- relate subtraction to taking away
- relate multiplication to repeated addition
- relate multiplication to a fraction "of" a number
- recognize that the commutative and associative properties apply to the addition and multiplication of fractions
|
Mastering math facts:
Understanding and recalling math facts, using a variety of strategies. |
Pattern Blocks+ can be used to:
- create arrays representing a product of two whole numbers
- apply knowledge of whole number facts to assist in recognizing patterns when operating with fractions
- practise number facts while solving problems involving Patterning and Algebra
|
Developing mental math skills:
Doing calculations in the mind, with little or no use of paper and pencil or calculator.
|
Using visual tools when learning to perform mathematical operations allows students to draw on these mental models and visualizations to perform mental calculations.
Students will develop their mental math skills with
Pattern Blocks+ as they:
-
determine the area and perimeter of blocks and composite shapes
-
solve problems involving the addition and subtraction of fractions and decimals
-
multiply and divide by 10 and 0.1
|
Developing proficiency with operations:
Performing calculations with ease, precision, and consistency and with a general understanding of number and operations, number properties, and their appropriate application in problem solving.
|
Pattern Blocks+ can be used to:
-
recognize the inverse relationship between addition and subtraction (e.g., since 1/6 + 1/3 = 1/2, then 1/2 - 1/6 = 1/3)
-
recognize the inverse relationship between multiplication and division (e.g., since 1/2 x 6 = 3, then 3 ÷ 1/2 = 6).
-
explain why dividing positive numbers by 0.1 gives a larger result
-
describe multiplicative relationships between quantities by using simple fractions and decimals
-
demonstrate an understanding of proportional reasoning using ratios and unit rates
|
Connecting Fundamental Math Concepts with mathies.ca (Draft)
top
Examples
Design
Students develop spatial sense by creating designs and copying or modifying existing designs.
Some possible activities include:
-
Create a picture of a flower using pattern blocks.
Note: This is a sample problem from the Grade 1 Geometry and Spatial Sense - Geometric Relationships expectation: compose patterns, pictures, and designs, using common two-dimensional shapes
-
Compose a hexagon using different numbers of smaller shapes.
Note: This is a sample problem from the Grade 3 Geometry and Spatial Sense - Geometric Relationships expectation: solve problems requiring the greatest or least number of two-dimensional shapes (e.g., pattern blocks) needed to compose a larger shape in a variety of ways (e.g., to cover an outline puzzle)
-
Create the design below:
-
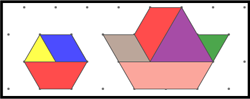
With the Dinosaur Template below, students could:
-
open the sample file with the grey image and cover it with blocks. Students could be asked to use the greatest and least number of blocks, or the greatest number of different blocks.
|
| On desktop, click on the image above to open this file. |
-
With the grey boat shape below, students could:
-
construct the shape by being told that it is similar to the brown boat block but with sides that are twice as long.
(older students could make conclusions about the angles in these two similar shapes)
-
open the sample file with the grey image and cover it with blocks.
Students could apply different rules (e.g., the covering blocks can go off the image, the covering blocks can overlap, gaps are not allowed).
|
| On desktop, click on the image above to open this file. |
-
open a file that has had questions added by their teacher.
-
place a brown block in various locations and find the centre of the dilatation that would produce the grey image.
-
create their own grey outline puzzle and challenge their classmates to cover it in a variety of ways (see instructions).
-
Search the web for tiling patterns that can be created using Pattern Blocks+. The Wikipedia article on polygon tilings is a good place to start. Describe the pattern core and the transformations required to extend the pattern. Identify the resulting symmetries (see three additional examples in the Geometric Properties section below).
top
Number Sense
Many of the
WINS counting activities can be used with Pattern Blocks+ (click the Activities link to expand the list).
Count the number of various types of blocks in a design.
Composing and Decomposing Numbers
See the
WINS activities for Composing and Decomposing
Numbers to 5,
Numbers to 10 and
Numbers to 20.
Comparing and Ordering Numbers
See the
WINS activities for Comparing and Ordering
Numbers to 10 and
Numbers to 20.
top
Geometric Properties
Sort a collection of shapes by their geometric properties.
(e.g., number of sides, side lengths, number of interior angles, number of right angles, area, perimeter, symmetry)
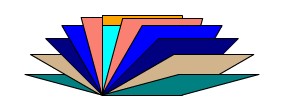
Students could be asked how the sort above was organized.
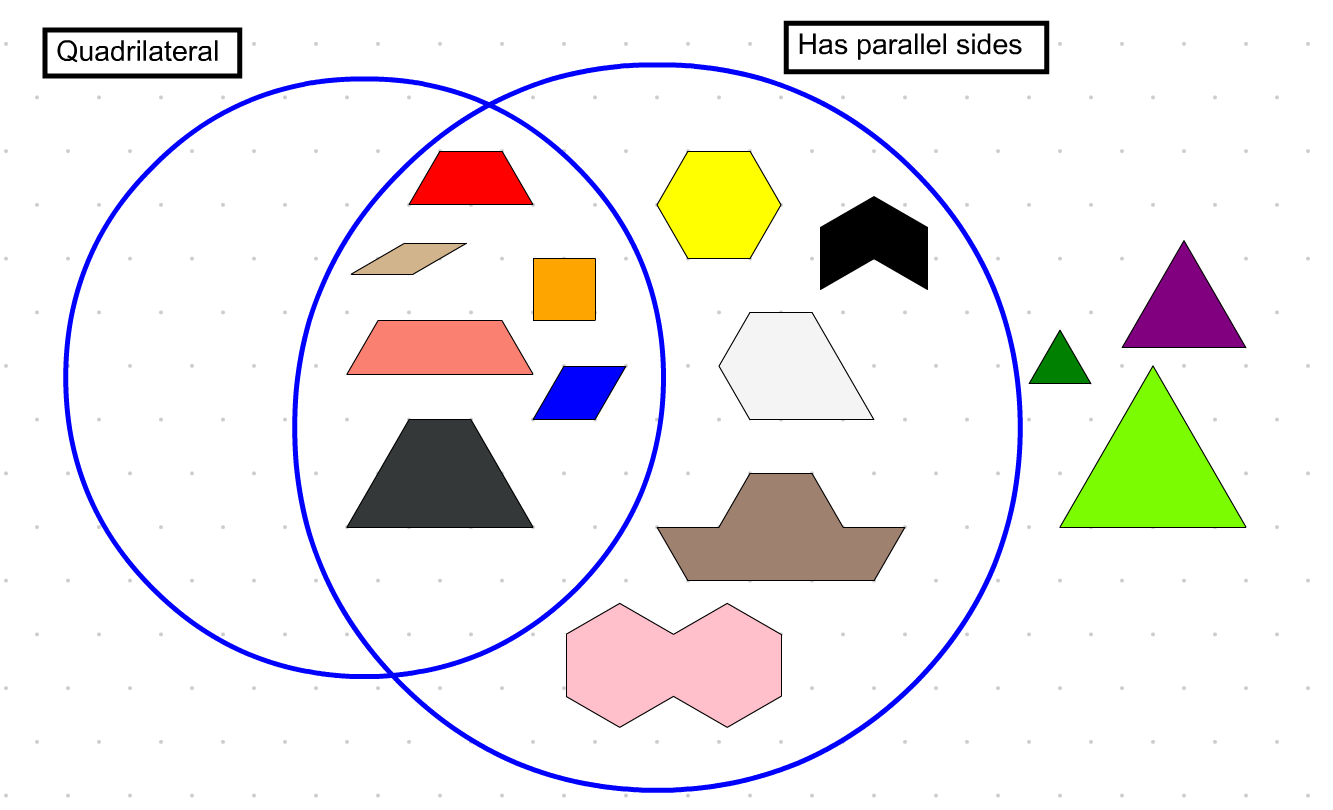
The sort above, using a Venn Diagram, raises some interesting questions:
- Is it possible for a quadrilateral to have no sides parallel? If so, use the annotation feature to draw one.
-
What other general classifications of shapes are not represented by a pattern block? (e.g., isosceles triangles)
Design new pattern blocks to represent some of those shapes. (e.g., an isosceles triangle with two 45° angles)
Challenges:
-
Is it possible to create a quadrilateral with no parallel sides composed of pattern blocks?
Reasoning using the interior angles of the pattern blocks might help.
Does the answer depend on whether blocks are allowed to overlap? snap to the grid?
-
Design a new pattern block that is a quadrilateral with no parallel sides.
Use triangular isometric grid paper (see NCTM's Dynamic Paper), dynamic geometry software or 2D design software, if available.
Possible Solution: The Geometer's Sketchpad was used to create a plum coloured quadrilateral block.
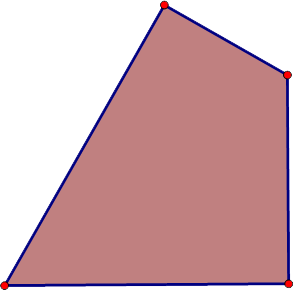
The design below was then created by:
- Inserting an image of the plum coloured quadrilateral block into the Pattern Blocks+ tool.
- Dragging a red trapezoid block into the workspace; rotating and resizing the plum block image to match one side length of the red trapezoid.
- Copying the plum block image and positioning it beside the original image.
- Dragging out and positioning the other blocks.
Notice: the two orange square blocks and a green triangle block are placed on top of the plum block image. Turn off snap to grid 
to place these blocks in the corners of the plum block. These corner blocks help us to see the 90°, 60°, 90° angles in three of the corners of the plum coloured block. What is the measure of the fourth angle?
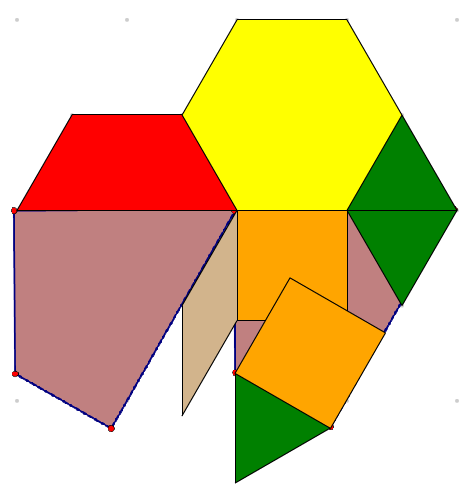
Create and identify congruent shapes.
In Pattern Blocks+, congruent shapes are created by copying, translating, reflecting and rotating shapes.
Students could also be asked to:
-
create each design using Pattern Blocks+
-
describe some of the transformations seen in the design
-
find the core shape that can be transformed repeatedly to create each design pattern
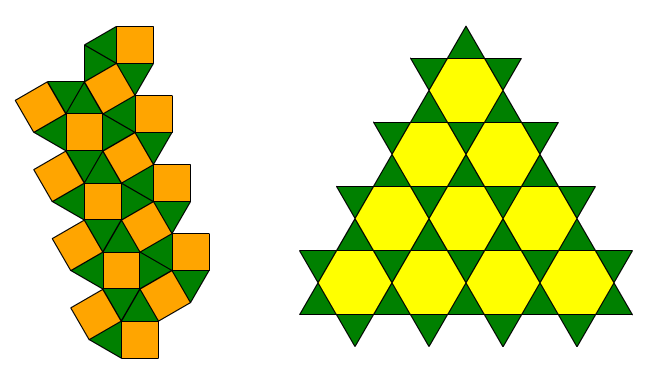Note: The first shape above can be accessed as a
sample file. Undo and redo through the sequence to see one way that the core can be identified and the transformations applied.
Guess my Shape.
Students work in partners. Each student creates a shape using pattern blocks, hidden from the view of their partner. Students then take turns providing clues that describe their shape using proper mathematical terminology. Based on the clue, the partner tries to replicate the shape. Students continue exchanging clues until each partner is able to replicate the other's shape.
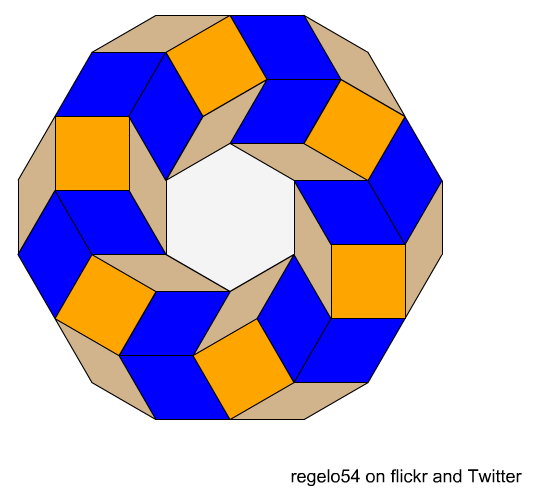
Some sample clues for the above shape:
- The shape is made up of six blocks.
- Each block shares a side with exactly two other blocks.
- All six blocks are congruent.
- There are more than 4 lines of symmetry.
What is the perimeter of this shape? (This question might spark some lively mathematical discourse!)
top
Patterning
Identify, extend, and create repeating patterns.
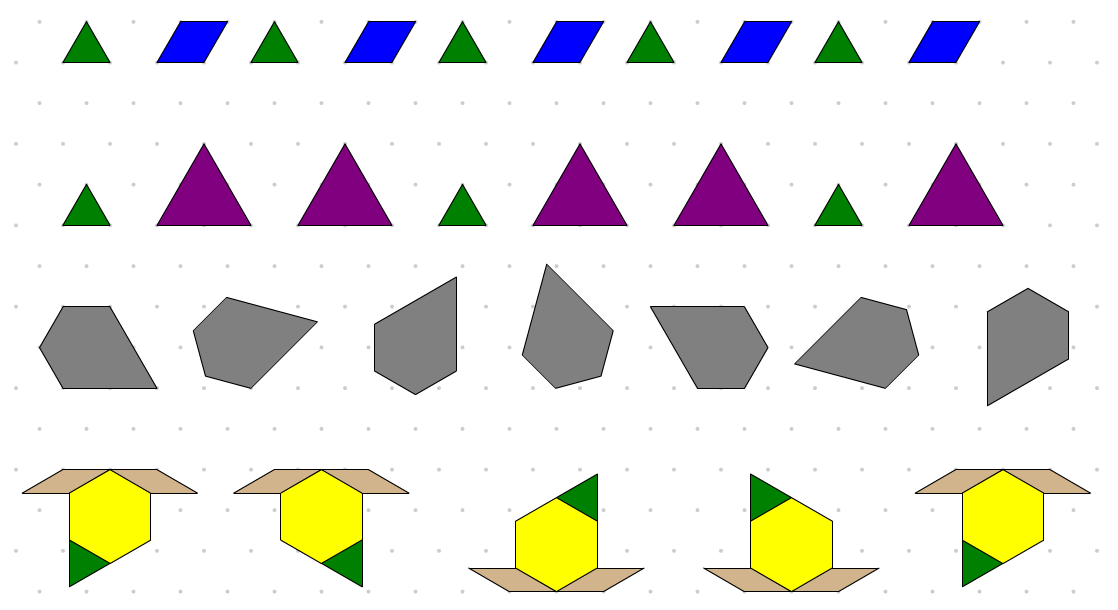
Students demonstrate an understanding that patterns result from using a transformation (e.g., slide, flip, turn), or making some other repeated change to an attribute (e.g., shape, size,
colour, orientation, number).
Note: In Pattern Blocks, all blocks with a given shape have the same colour, limiting the number of attributes that can change. To create patterns with more attributes, consider using the
Set Tool.
Students extend and create repeating patterns that result from reflections and/or rotations.
Create a pattern block train by alternating one green triangle with one red trapezoid. Predict which block will be in the 30th place.
Note: This is a sample problem from the Grade 4 Patterning and Algebra - Patterns and Relationships expectation: make predictions related to repeating geometric and numeric patterns
Identify, extend and create growing patterns.
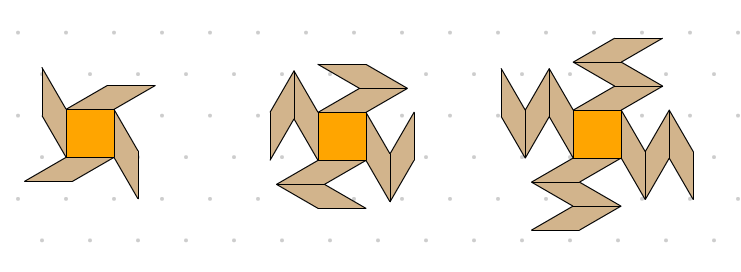
The image shows the first 3 terms of a linear growing pattern.
What will the 10th term look like?
How many blocks will be in the 10th term?
How many blocks will be in the 100th term?
Does a term exist which contains 45 blocks? 300 blocks?
Students create visual representations of linear growing patterns then pose and answer questions about each pattern.
top
Measurement and Geometry
The Ontario Curriculum (
Link #2) suggests using physical pattern blocks as non-standard units of length, area and volume.
Covering designs (see
above) also addresses a variety of Geometry expectations found in the Ontario Curriculum.
Students take measurements of composite shapes and relate them to side lengths, areas and angles of basic blocks.
Length and Area Units used with Pattern Blocks
The Pattern Blocks+ tool uses a triangular isometric grid.
A typical
length unit is the distance between adjacent dots, which is a side length of the first six standard pattern blocks.
A typical
area unit is the area of the small green triangle.
When a 1cm by 1cm square grid is used, lengths would typically be measured in centimetres and areas in square centimetres.
On the Pattern Blocks+ grid below, the small green triangle's area is not the square of its side length. It is the orange block that has area equal to the square of its side length.
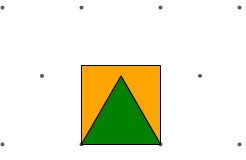
The square's area is more than twice the area of the triangle.
Hint: Draw a vertical line through the middle of the shape.
More precisely, the area of the small green triangle is about
43% of the area of the orange square.
Area of the Yellow Hexagon - Two Approaches
When we say that the yellow hexagon's area is 6, we mean 6 little green triangle areas.
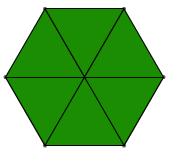
However, the yellow hexagon's area, measured in orange square areas, is less than 4, as illustrated by the image below.
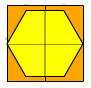
The yellow hexagon's area is actually less than 3 orange square areas.
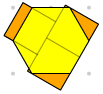Hint: Compare the area of the hexagon that is not over squares to the area of the squares that is not under the hexagon.
When measuring, it is very important to be clear about the units being used. The yellow hexagon measures 6, when the area of the small green triangle is the unit. However, it measures approximately
2.6, when a square grid unit is used.
top
Example 1 - Greatest Perimeter for a fixed Area
Create a composite shape using six yellow hexagon blocks with the greatest possible perimeter.
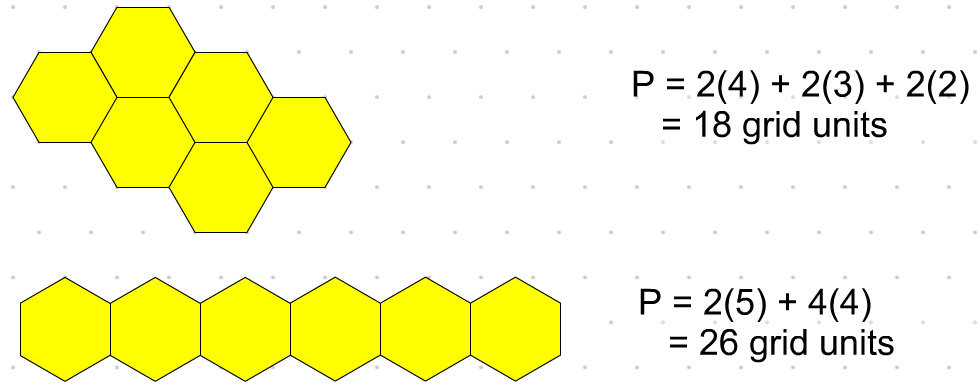
Encourage students to use efficient computational strategies to calculate the perimeters.
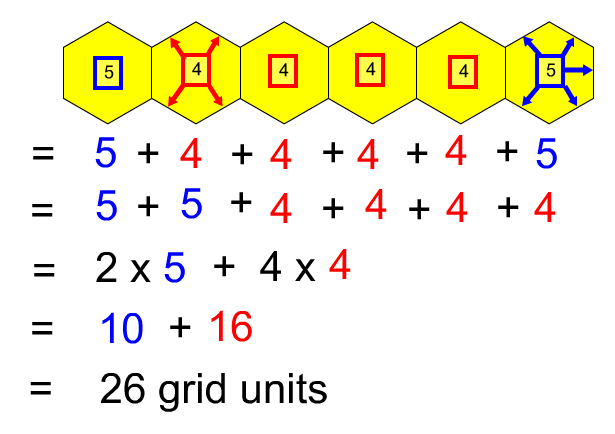
Extensions:
- Change the number of blocks allowed to make the composite shape.
- Change the type of blocks allowed to make the composite shape.
- Create composite shapes with the greatest possible area for a given perimeter.
- Identify angles of 60°, 120°, 240°, and 360° in the composite shapes created.
top
Example 2 - Relating the Area of a Triangle, Parallelogram and Rectangle
Relate the area of a triangle to a parallelogram.
Reason that the parallelogram (in this case a rhombus) has twice the area of the large green triangular block by:
-
recognizing that the parallelogram is made up of two congruent large green triangular blocks
-
counting the number of small green blocks in each (9 and 18)
Relate the area of a triangle to a rectangle.
-
Use the annotation feature to draw a blue rectangle around the light green triangle. Draw solid triangles in the white space. Rotate them to fit inside the triangle.
-
Reason that the rectangle has twice the area of the light green triangle.
Relate the area of a parallelogram to a rectangle.
-
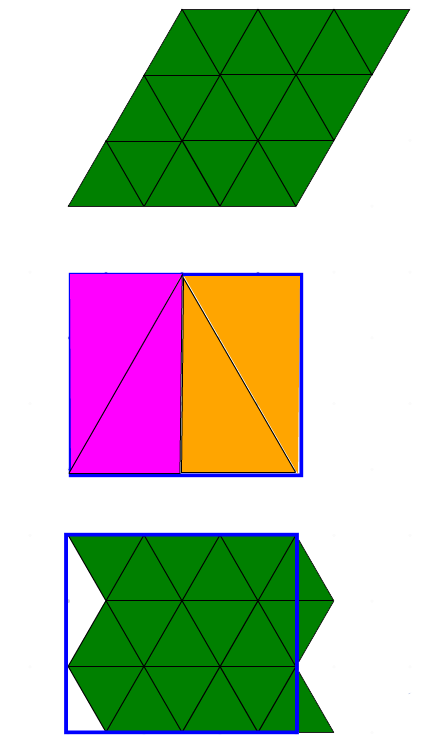
Reason that the area of the parallelogram is the same as the area of the rectangle since they are both twice the light green triangle.
-
Use the small green blocks to confirm that the number of blocks required to cover the parallelogram will also cover the rectangle.
Like many activities involving Pattern Blocks, this activity is meant to give students an introductory, visceral experience of the area relationships above, which can then be extended to more general cases.
top
Example 3 - Angle Measures
Determine the interior and exterior angles of all the pattern blocks by relating them to the equilateral triangle's interior angles of 60°.
e.g., Deduce that the angles in the tan rhombus are 30° and 150°.
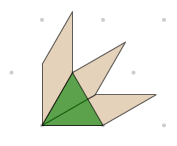Verify properties including:
- a straight angle is 180°
- the angles in a triangle sum to 180°
- the angles in a quadrilateral sum to 360°
- an exterior angle of a triangle is equal to the sum of the two opposite interior angles
top
Example 4 - Similar Figures
Relate the areas and perimeters of similar shapes.
For example:
-
the grey boat has twice the perimeter of the brown boat block and four times its area.
-
the large light green block has three times the perimeter as the small dark green block and nine times its area.
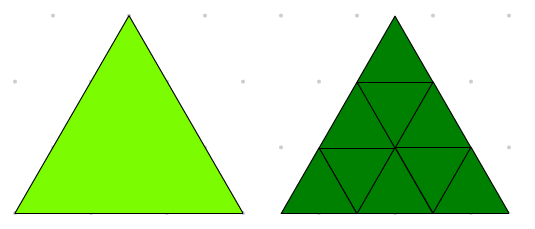
top
Example 5 - Height of an Equilateral Triangle
Note: When one side of a triangle is identified as the
base,
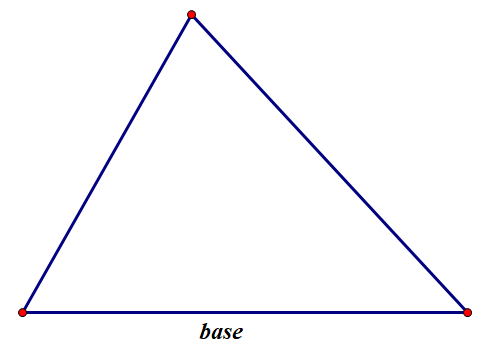
then the segment perpendicular to the base containing the opposite vertex is called the
height or
altitude of the triangle.
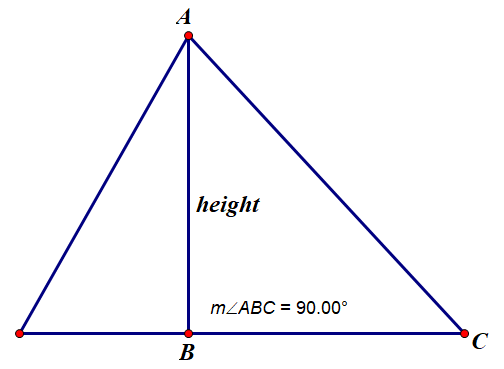
In Grade 7, students will learn that no matter which side is treated as the base, the area is one-half the length of the base multiplied by the height from that base.
Relate the height of the green triangle block to its side length.
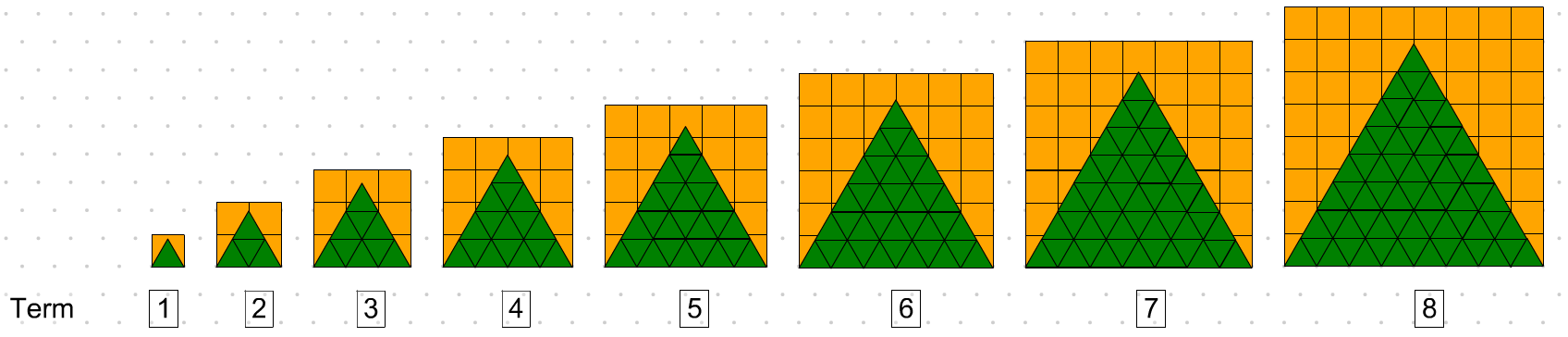Click the image above to see it at full size, without distortion.
From each numbered term above, reason that the height is:
- less than its side length
- more than one-half its side length
- more than two-thirds its side length
- more than three-fourths its side length
- more than four-fifths its side length
- more than five-sixths its side length
- really close to six-sevenths its side length
- less than seven-eighths its side length
Use the Pythagorean theorem to relate the height of the green triangle block to its side length.
The
difference between the estimate of six-sevenths and the actual value is less than 1%.
Create various number patterns from the sequence above.
- number of squares
- number of triangles
- number of pattern blocks
Solve related problems (e.g., what is the next term, the 20th term, the general term).
Fun facts about triangles
(that have precious little to do with Pattern Blocks)
The three altitudes of a triangle always intersect in a single point called the
orthocentre of the triangle. This point is the centre of a circle that can be constructed by creating a triangle with sides parallel to the original triangle through its vertices (see below).
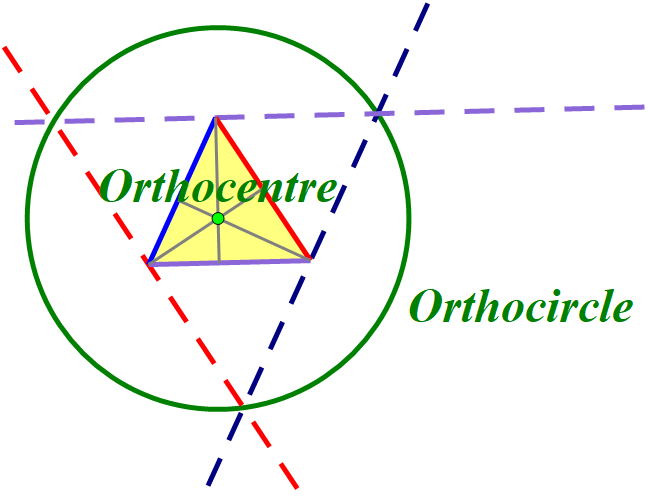
Other "
centres" of a triangle include the circumcentre, incentre and centroid, although for an equilateral triangle these are all the same.
|
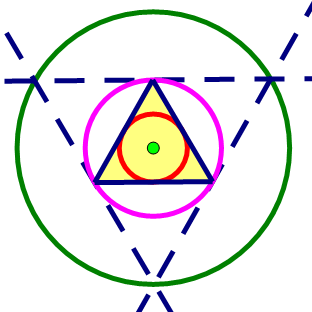
A yellow equilateral triangle with the
red incircle, purple circumcircle and green orthocircle constructed |
top
Fractions and Decimals
What fraction of the area of this figure is green?
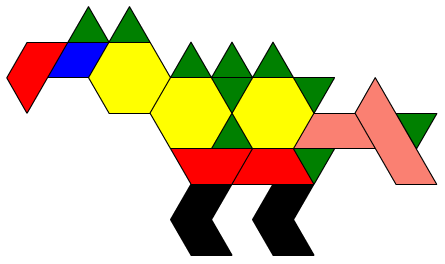
Students use an area model to determine the fraction.
Students might:
- identify the green triangle as a unit piece that could be used to cover the entire figure,
- count the number of green triangles required to cover the entire figure (55),
- name a green triangle as a unit fraction (1/55),
- count the total number of green areas using the unit fraction (e.g., 1/55, 2/55, 3/55, … , 10/55), and
- recognize that this count gives the correct fraction (10/55 of the shape is green).
Students could also be asked:
- whether the yellow area is greater than the green area?
- what fraction of the blocks are green? (a set model)
- to create a shape that is five-sixth green.
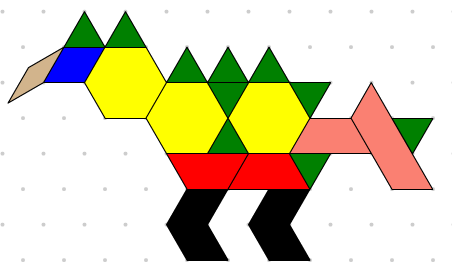
Note: This shape was created by using the
Dinosaur sample file and replacing the tan rhombus with a red trapezoid so that the area can be expressed in terms of the green triangle.
Naming Fractions
|
|
|
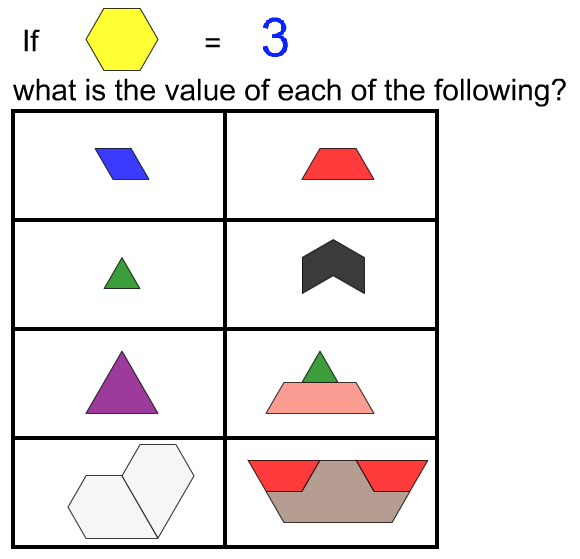
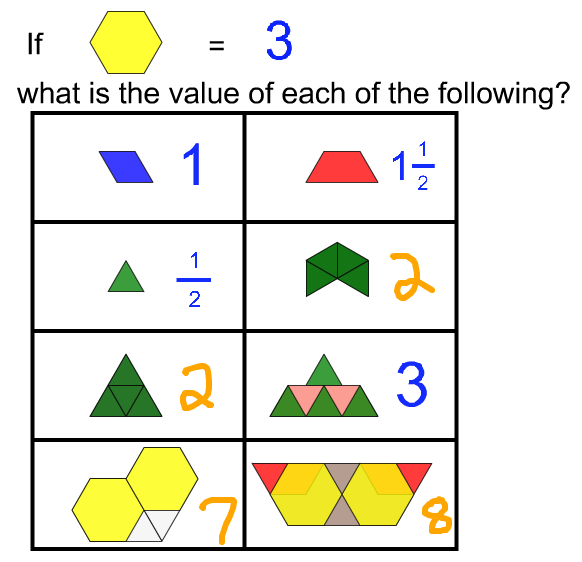
On desktop, click on the image above to open this file.
|
Answer Key
|
Much as students might use
Relational Rods to compare various lengths, they can use Pattern Blocks to compare the areas of various shapes, using fractions.
This example can be changed by:
- swapping out the hexagon for a different shape made up of one or more blocks
- swapping out the "3" with one of the other images in the .zip file created for this purpose, or with any fraction drawn freehand
- using different shapes in the table
Students could challenge each other, "I have two shapes. The area of one shape is one-eighth and the area of the other shape is three-fourths. What might my two shapes be?"
Or, for a real challenge, use one-fifth and three-fourths.
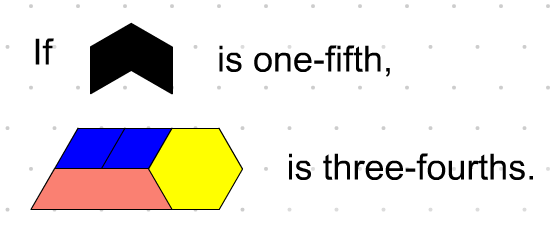
See the
Changing Wholes with Pattern Blocks task from the
Fractions Learning Pathways.
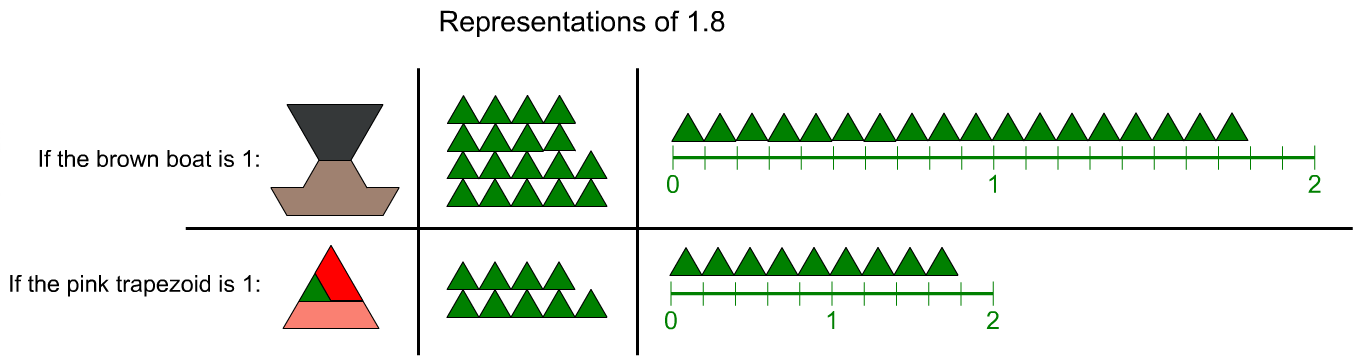
Decimals
Pattern Blocks+ can be used to represent decimals.
Represent 1.8 in more than one way
Represent and calculate 0.5 ÷ 0.1
top
Algebra
Create expressions and solve equations.
For a collection of triangles, the total number of sides is equal to three times the number of triangles or
s = 3
n.
Note: This is an example from the Grade 8 Patterning and Algebra - Variables, Expressions, and Equations expectation: translate statements describing mathematical relationships into algebraic expressions and equations
Solve problems related to pattern rules.
PB Industries manufactures boat-shaped tables. Write an expression for the number of seats,
s, for
t tables. How many tables are needed to seat 100 people?
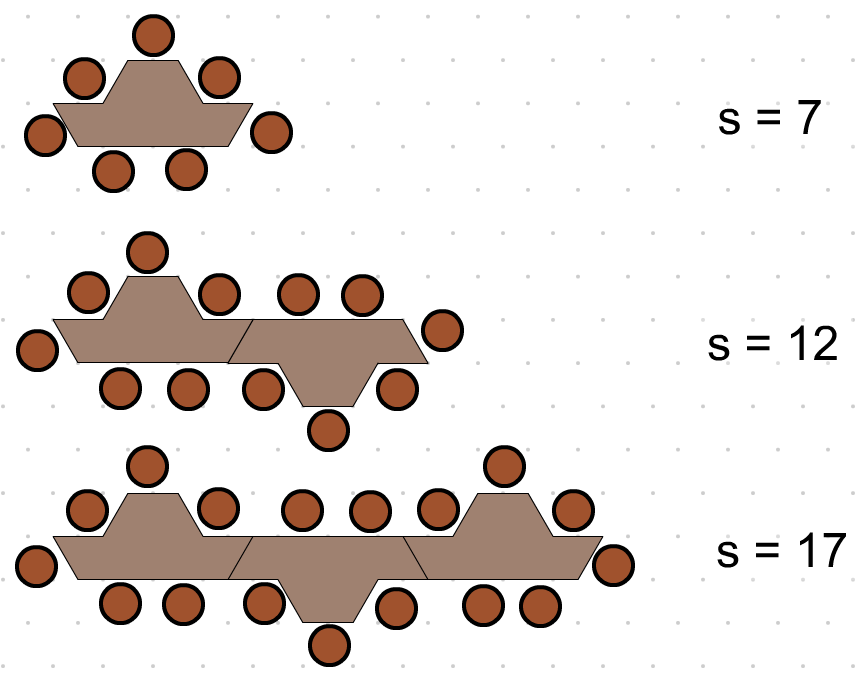Assign values to various blocks and come up with expressions, substitute values into those expressions and solve equations involving those expressions.
PB Industries is creating pattern blocks from scrap material.
It determines that its cost to produce a pattern block is $0.05 per cut.
Arrange the blocks from least expensive to most expensive.
The ordering of the first fourteen pattern blocks shown below assumes that a cut is made for each side of the block.
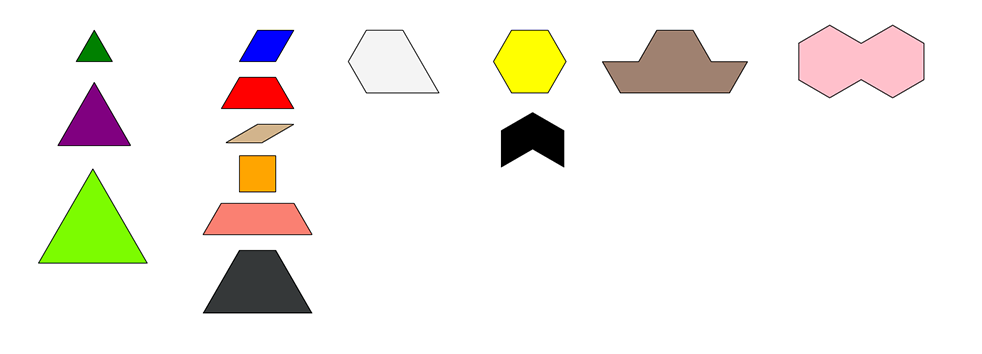
A contractor decides to tile a floor using PB Industries' blocks.
If the contractor only cares about coverage for the cheapest price, which blocks should be used the most?
A student might reason that the block of greatest area for each group would be the most cost-efficient and then sort those blocks from most cost-efficient to least cost-efficient.
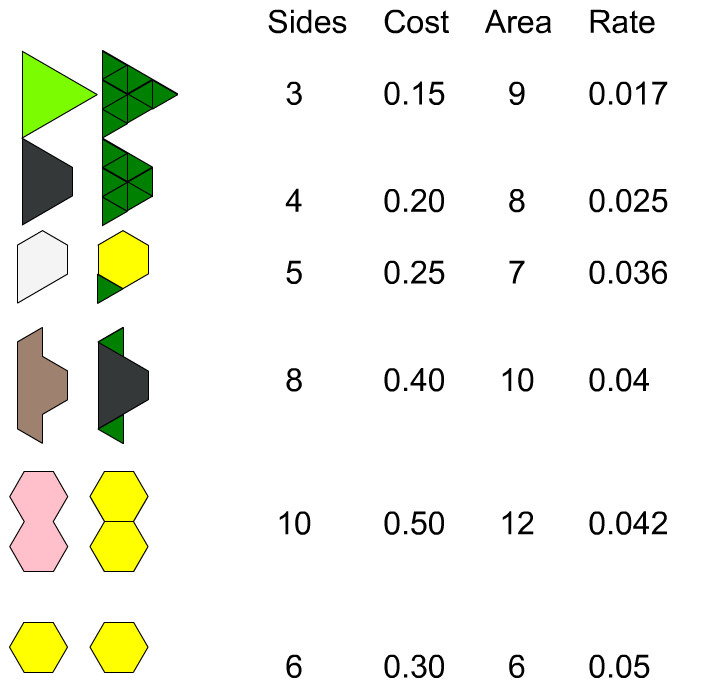
To compare the cost-efficiency of these six blocks, a rate calculation is made. What does the rate of 0.05 mean for the hexagon?
Extensions:
- Write the relationship between cost and number of cuts as a linear function. Graph that function. Create a composite shape that would cost $1.
- Determine how the situation would change if material costs $0.12 per sq. cm, and the smallest block is an equilateral triangle with side length of 1 cm.
- Compare the costs of various tiling patterns for a room that is 5m by 3m.
top
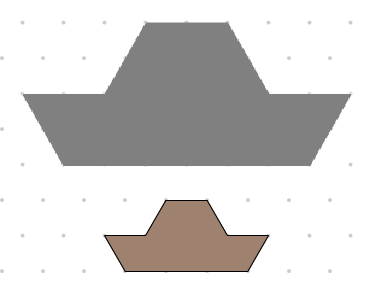
Create an Outline Puzzle
Create an outline puzzle, or template, similar to the
grey boat example above, and then challenge others to cover it with pattern blocks (see Grade 1 Curriculum connections [
Link #2]).
Creating an Outline Puzzle using mathies Pattern Blocks+ (PDF) describes how to turn
a block design like
into an outline puzzle template like
.
top
Sample Files
To access a sample file:
-
click the link in the Sample column (desktop only), or
-
use the Open WWW button
in the Settings dialog and supply the URL, or
-
download the file from the URL column (right-click and save locally on desktop, hard tap on mobile) and use the Open button
in the tool, or
-
add the mathies sample files Google drive folder to "My Drive" which allows convenient access on all devices.
See the
File Operations page for more details.
Note: These files were designed on a desktop computer and may not open exactly as shown on other devices.
top
Features of the Tool
| Button |
Description |
|
|
Block Size
Decrease / increase the block size.
|
|
|
Snapping
Pattern Blocks snap to each other and to the isometric grid unless this setting is toggled off. When this setting is toggled on, shapes rotate to multiples of 15°.
|
  |
English / French
Switch between English and French.
|
|
|
Annotation Tool
Hide / Show a wide variety of Annotation Tools which can be used to communicate thinking.
|
|
|
Insert Image Button
Insert images into the tool. More details.
|
|
|
Undo / Redo
Step backward or forward through the actions taken with the tool.
This feature is not only useful for backtracking when a misstep is made, it enables a student to demonstrate their work from the start to the finish. The student can press Undo until they are at the start of their solution and then press Redo repeatedly, explaining each step.
Note: Undo / Redo is not available for annotation objects.
|
|
|
Reset
Delete all work and return the tool to its starting state.
|
|
|
Information
Shows a dialog with a link to this support page, a feedback form as well as copyright details and version number.
|
|
|
Settings
Shows the settings dialog.
The Auto Size Annotation setting is selected by default. This means that if the block size is changed, any annotation in the workspace will be
scaled to match.
The Apply Template Settings button is used to turn composite shapes into one grey shape with no visible outlines. See Creating Outline Puzzles for more details.
The Use Standard Colours button is used to restore the default block colours. Use the Restore Defaults button to restore all the settings, including block colour.
Open, Import and Save files (see File Operations for more details)
|
|
|
Recycle
(in the workspace)
Click to clear selected blocks. If nothing is selected, the entire workspace will be cleared.
Alternatively, drag items to the recycle bin to remove them.
|
|
|
Block Count
Show / Hide counts next to each cloner block. Scroll to see all the blocks and their counts.
|
|
|
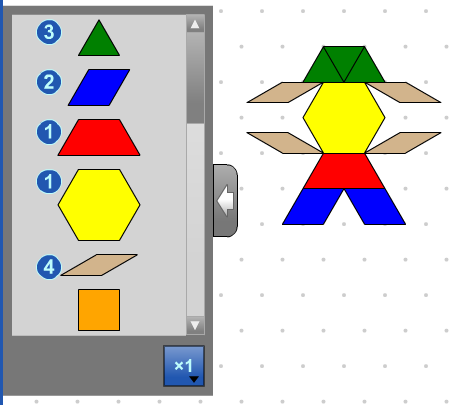
Number of Copies to Drag
Set the number of copies to drag from the selection panel.
|
|
Copy
Make a copy of the selected objects.
|
top
Other Functionality
|
|
Multiple Select
To select blocks draw a marquee rectangle around them.
Hold down the SHIFT key when drawing a marquee rectangle to add to the previous selection.
Click a block to add or remove it from the selection.
Selected blocks can be moved, copied, rotated, reflected vertically or horizontally, or recycled as a group.
|
|
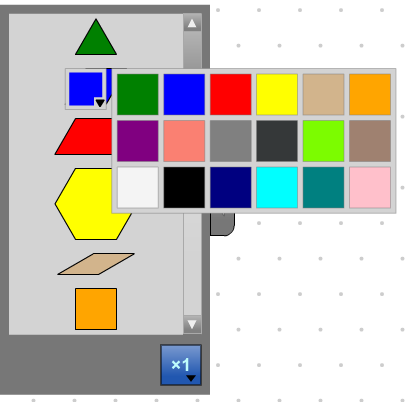
Configure the Selection Panel
Click on a cloner block in the selection panel to change the colour of all blocks of that type.
|
top
Keyboard Shortcuts
On the desktop version of this tool, the standard
Keyboard Shortcuts have been implemented.
Links
PDF supports
-
Focusing on the Fundamentals of Math - A Teacher's Guide
-
Pattern Blocks Curriculum Links
-
Connecting Fundamental Math Concepts with mathies.ca (Draft)
-
Creating an Outline Puzzle using mathies Pattern Blocks+
-
mathies Tools and Games used in WINS
-
Pattern Block Template
-
Pattern Blocks Manipulative Sheet
(Source - EduGAINS | Ministry Developed Resources | Mathematics | Lessons & Supports | Manipulatives)
- What are Pattern Blocks?
- How do Pattern Blocks help students?
- Sample Activities
- Recommended Websites (dated)
Visit EduGAINS for additional Manipulative Sheets.
top
Algebra Tiles
Colour Tiles
Fraction Strips
Money
Notepad
Number Chart
Pattern Blocks+
Rekenrek
Relational Rods+
Set Tool
