|
button. |
| E.g. Insert a screen cast of the question you are working on. |
 |
Values can be thought of as:
|
 |
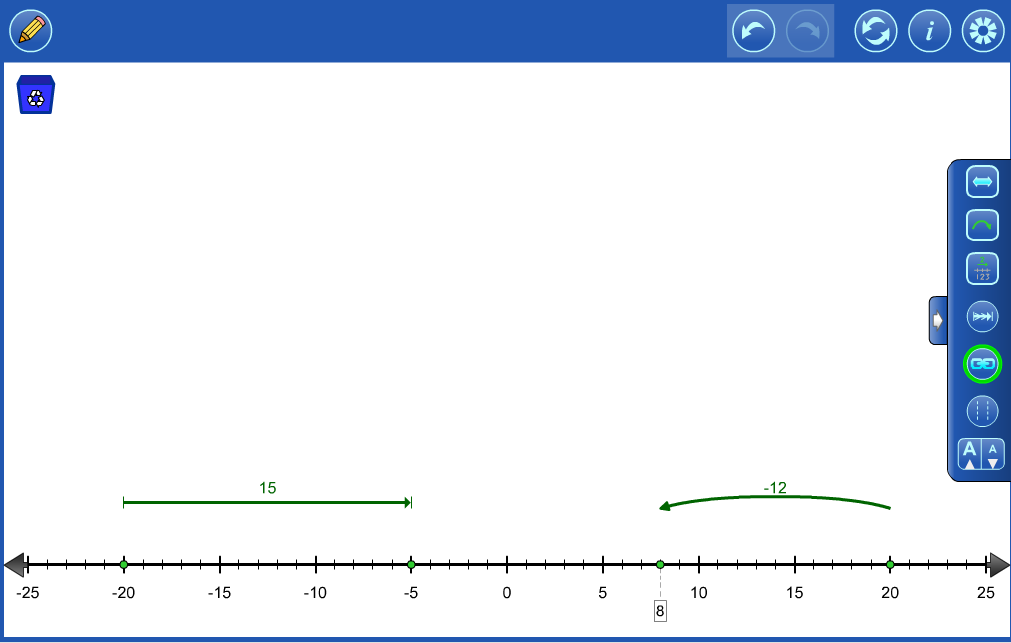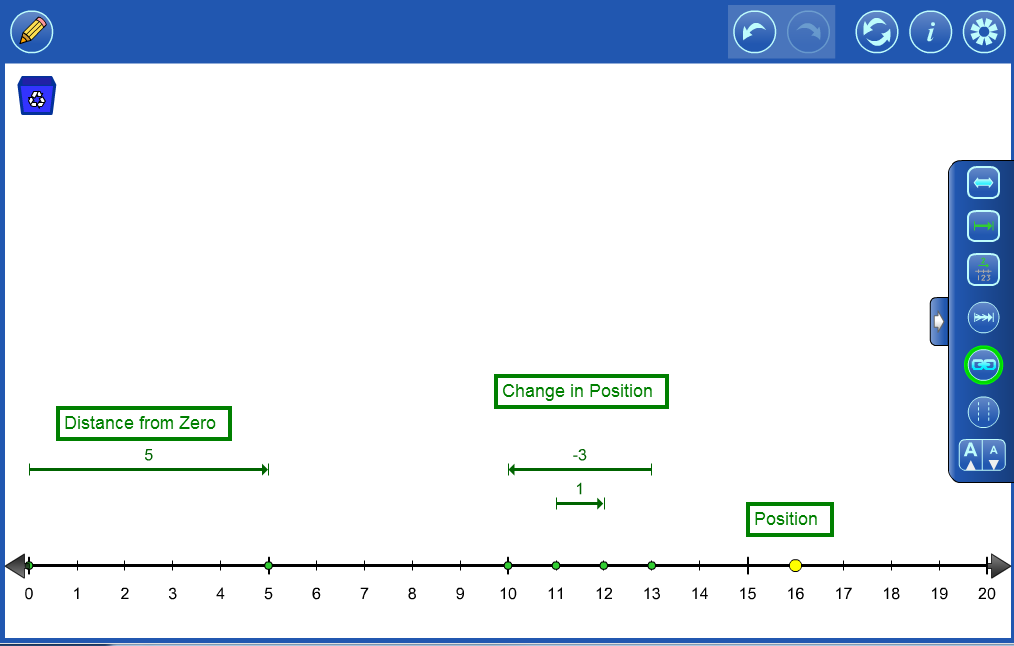
Vectors or hops can be used to represent directed values. |
 |
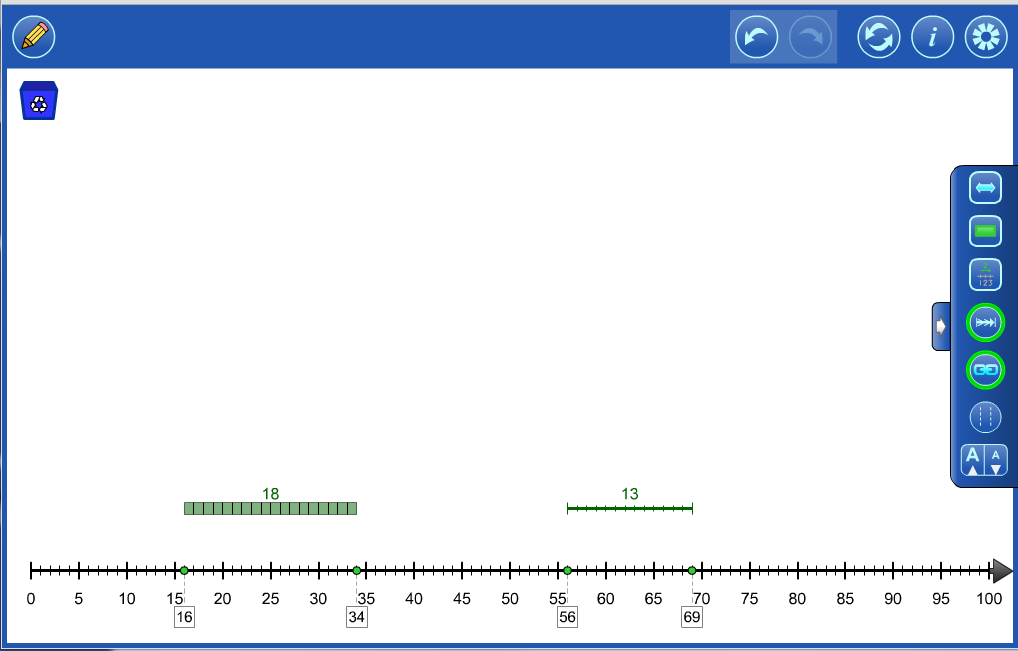Ribbons or magnitude bars can be used to think about only the number's magnitude.. |
 |
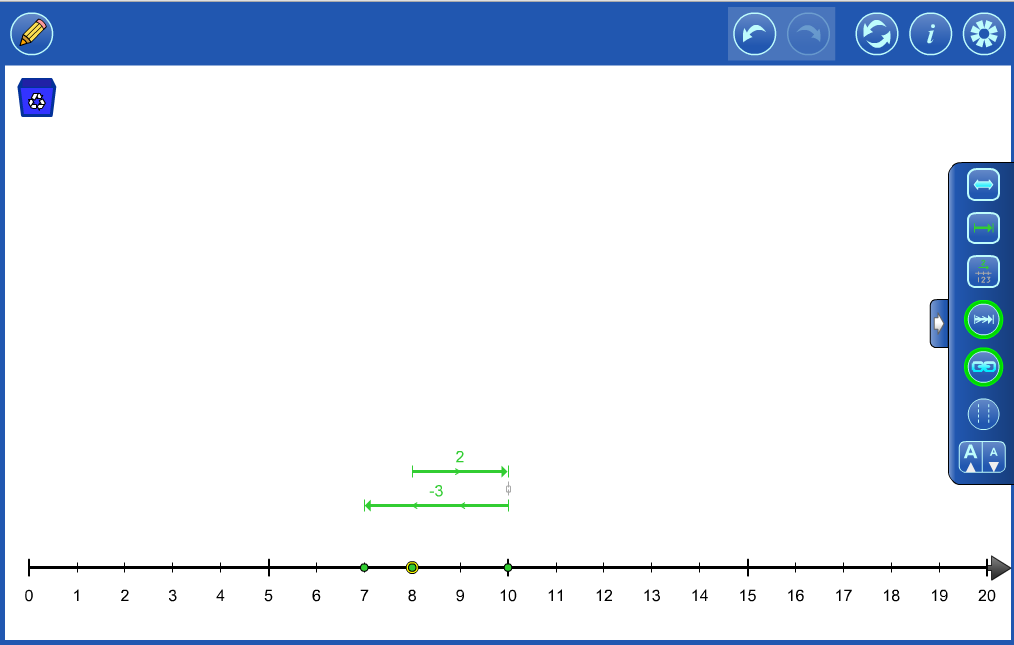Objects can be linked together to model a story. eg. Sandy had 8 cookies. Her mother gave her two more, then she gave three to her brother. |
 |
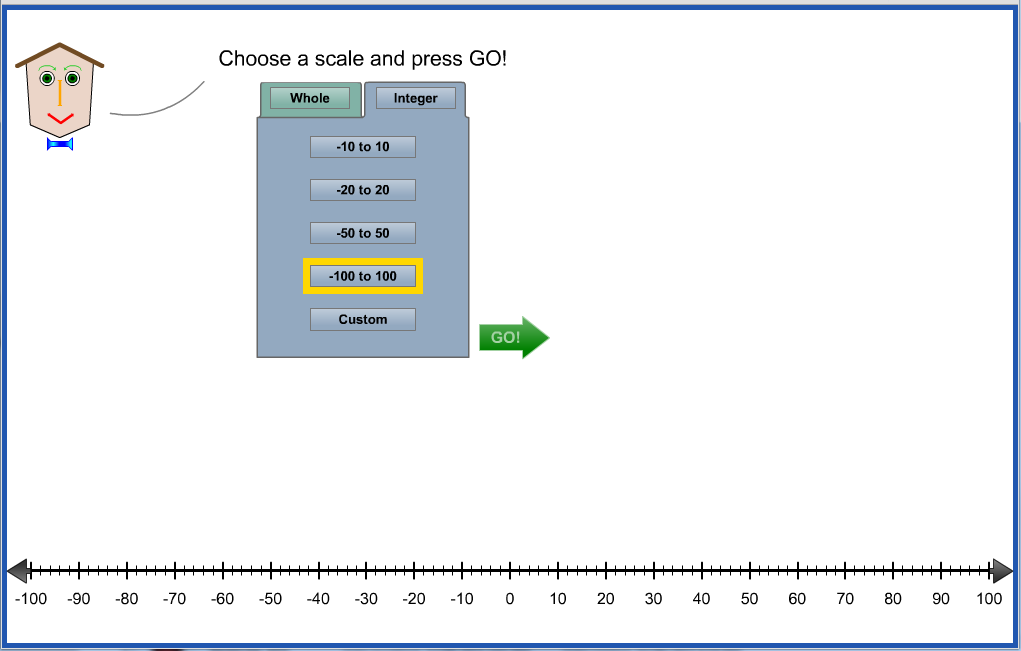Initially, the tool opens with whatever scale was selected from the opening screen. |
 |
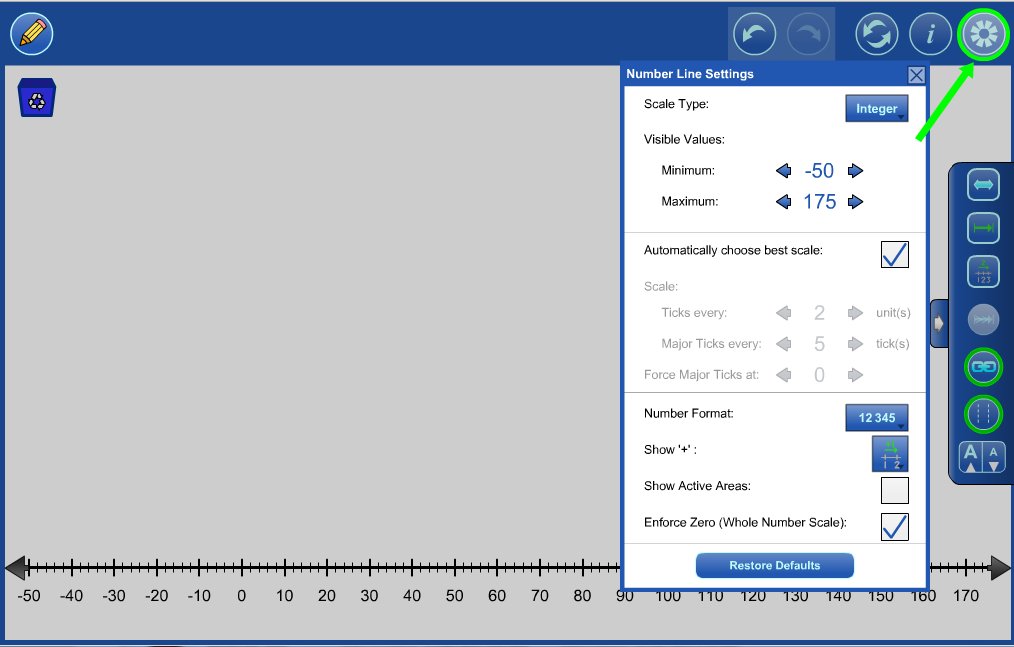Click the settings button to adjust this scale. Set the Minimum and Maximum values. |
 |
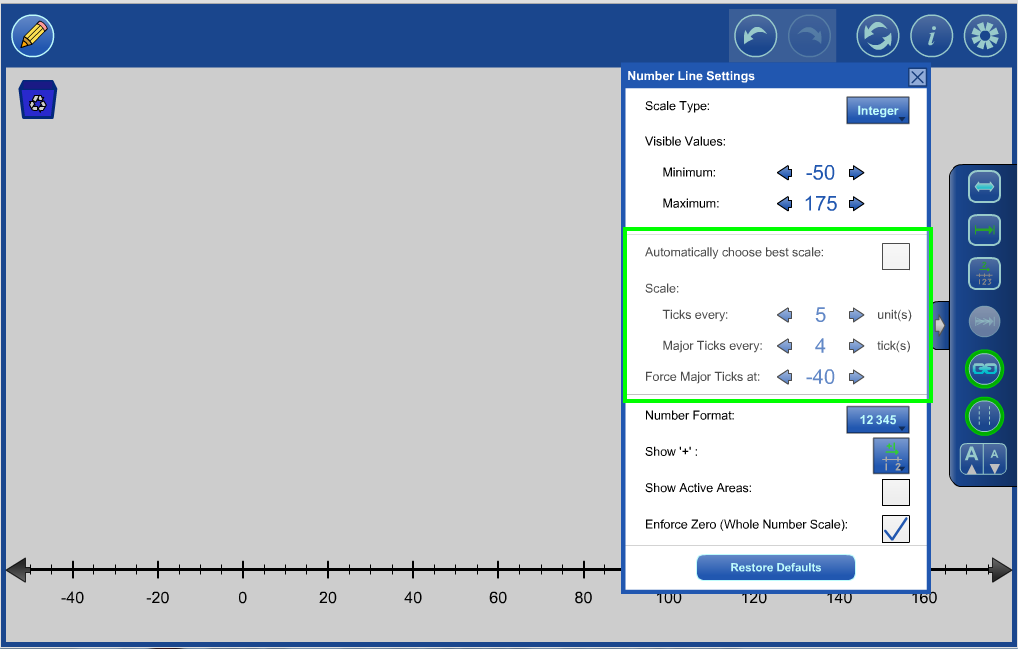Turn off automatically choose best scale to further customize the scale. |
 |
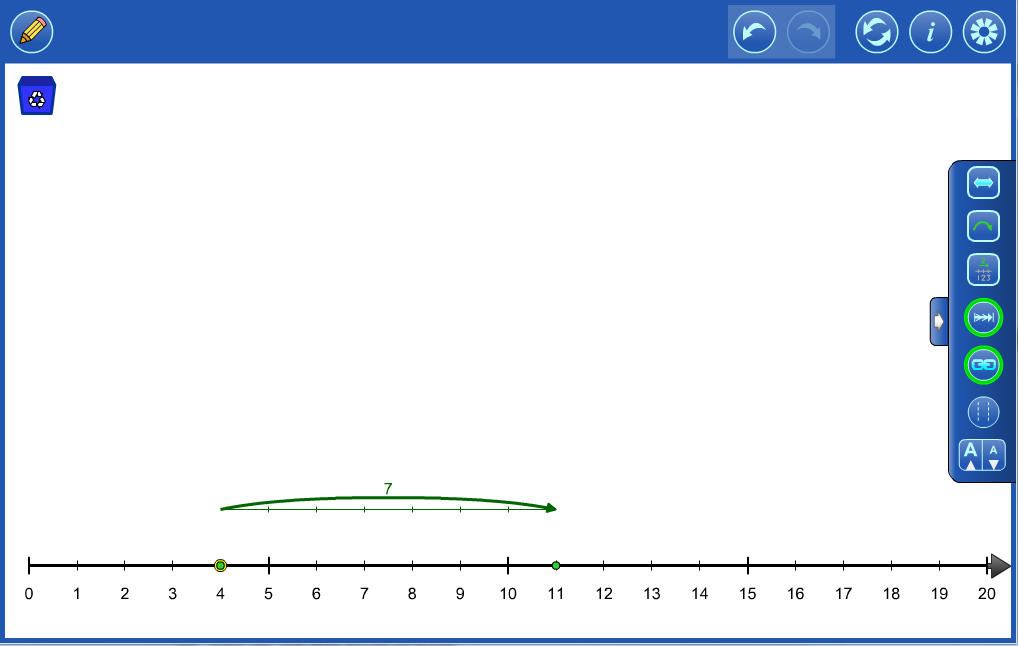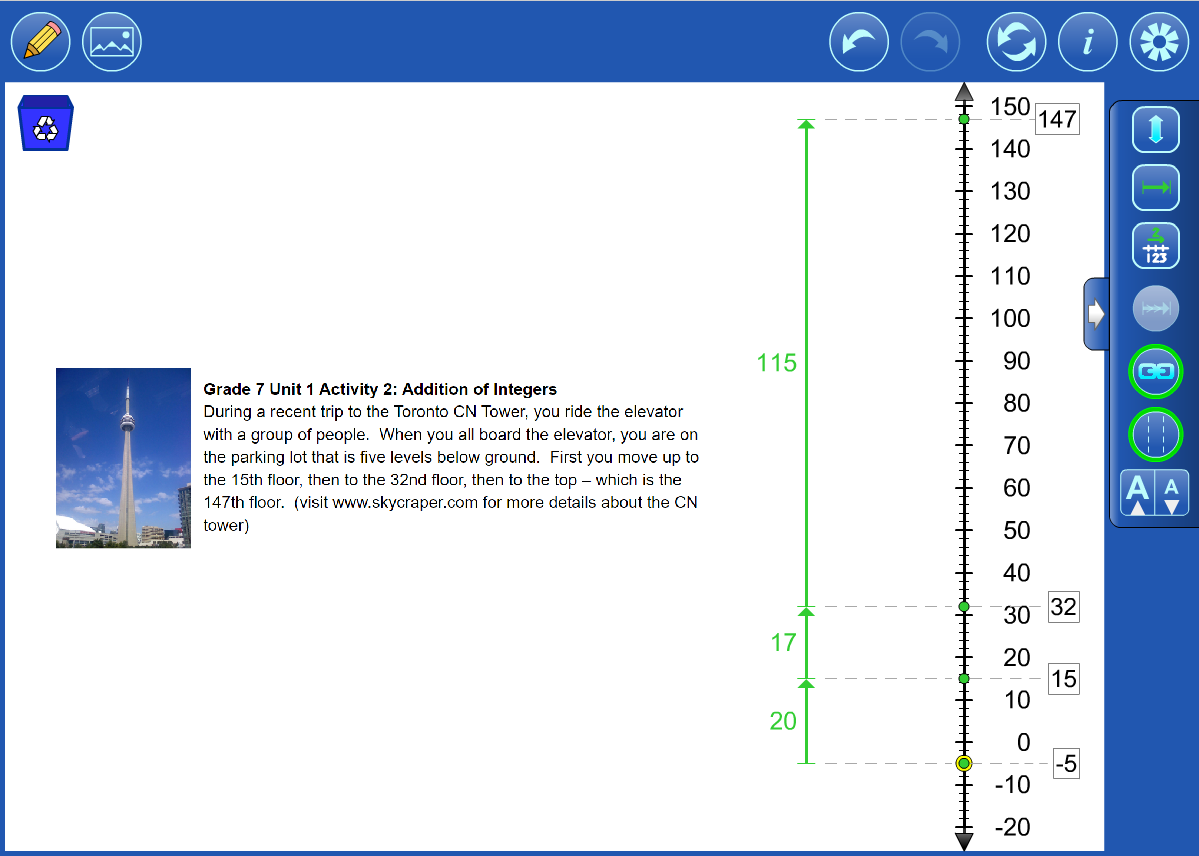
Whole Number Example 1 There were 4 birds in a tree and then some more birds landed in the tree. Now there are 11 birds in the tree. How many more birds landed in the tree? |
 |
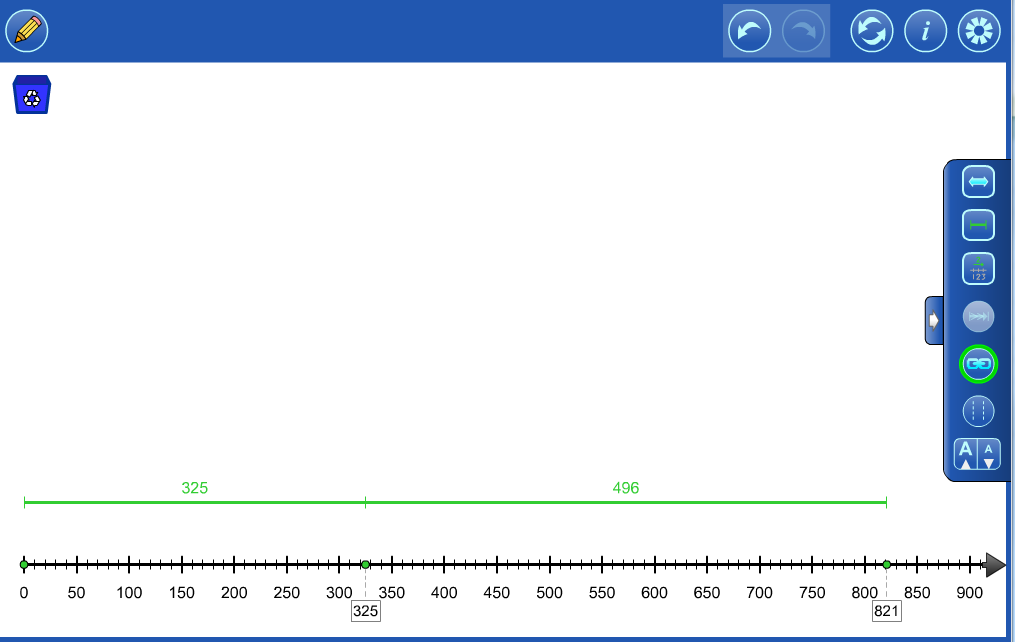Whole Number Example 2 Bob combined two Lego kits. One kit had 325 pieces and the other had 496 pieces. How many pieces does he have in all? Use math tools or models to justify your answer. |
 |
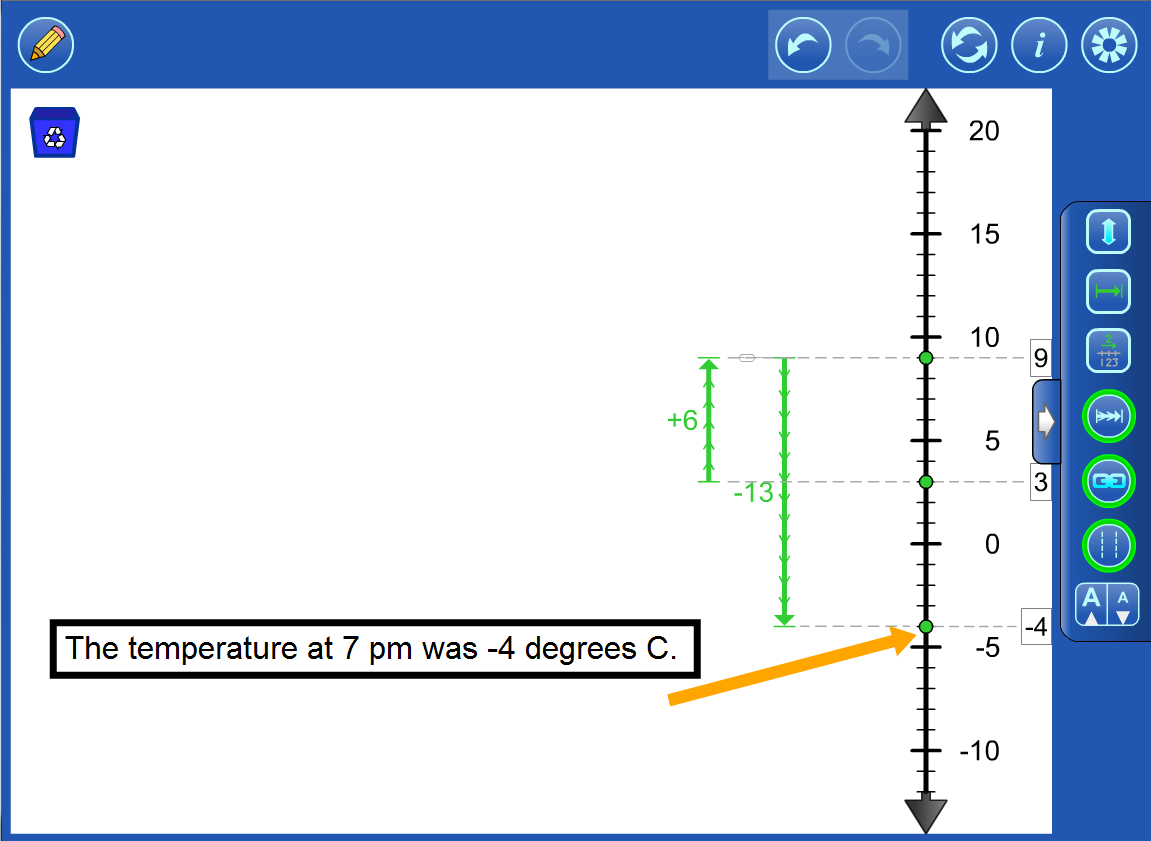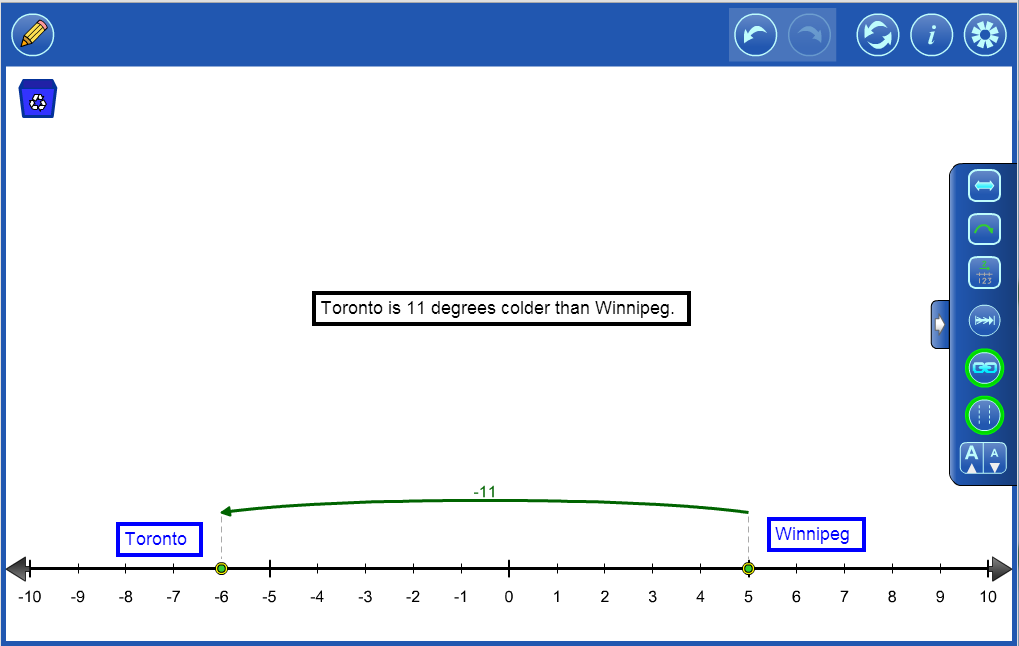
Integer Example 1 The temperature at 7 am was +3°C. It rose 6°C by noon and then dropped 13°C by 7pm. What was the temperature at 7pm? |
 |
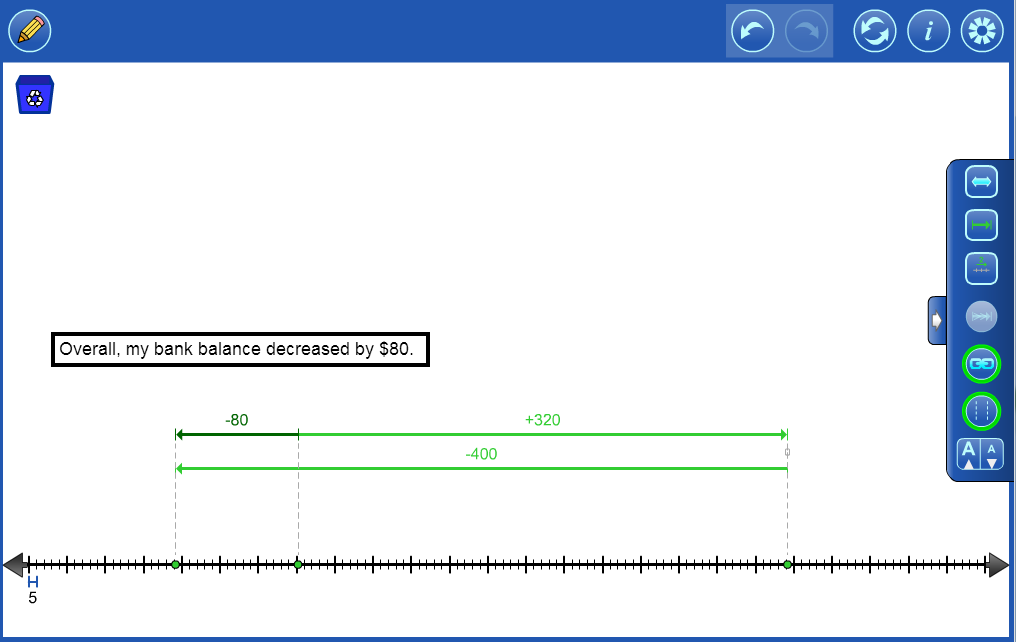Integer Example 2 I deposited a cheque for $320 dollars and then withdrew $400. What is the overall change in the value of my bank balance? |
 |
 |
Annotation ToolMake notes or highlight various features of your representation. More details. |
|
Insert Image ButtonYou can insert images into the tool (as of version 1.1.0). More details. |
 |
Undo/RedoStep backward or forward through your actions with the tool.This feature is not only useful for backtracking when a misstep is made, it enables a student to demonstrate their work from the start to the finish. They press Undo until they are at the start of their solution and then press Redo repeatedly, explaining each step. |
 |
ResetDelete all your work and return the tool to its starting state. |
 |
InformationAccess a link to this support page, a feedback form as well as copyright details and version number. |
 |
SettingsAdjust scale, number format, where + signs show.Hide/show active areas.Restore the tool to its default settings. |
 |
Recycle(in the work space)Click to clear the entire work space.Alternatively, drag items to the recycle bin to remove them. |
 |
Recycle(a specific object)Click to remove the selected object. |
 |
Number Line Button PanelThis collapsible panel provides easy access to all of the Number Linespecific settings described in detail below.Green highlights indicate that the setting is active. Click the white arrow to hide/show the panel. |
 |
Number Line OrientationSwitch between a horizontal or a vertical number line. |
 |
Representation ObjectsChoose between vectors, hops, ribbons or magnitude bars. |
 |
LabelsHide/show labels on representation objects and/or number line. |
 |
Unit TicksHide/Show unit ticks on the representation objects. |
 |
Object LinkingAllow/disallow the linking of representation objects.Linked objects move as one entity.Objects that are linked together are shown in light green. Objects that are not linked together are shown in dark green. |
 |
Drop DashesHide/show drop dashes from the ends of the objects to the number line. |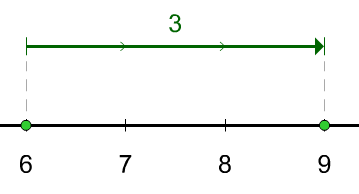
 |
Label SizeIncrease/decrease label size. |
Zoom in on a position by
|
|
Zoom out by
|
|
Zoom to fit by
|
|
To pan
|
|
Algebra Tiles
Colour Tiles
Fraction Strips
Money
Notepad
Number Chart
Pattern Blocks+
Rekenrek
Relational Rods+
Set Tool