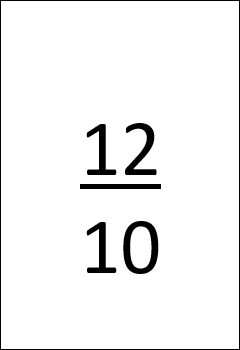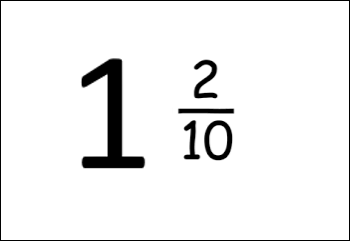Jeux de cartes de représentations

English version of this page

Le contenu

Les compétences et concepts fondamentaux en mathématiques
Activités

• Jeux d'associations
• Jeux de quantités et de chiffres
• Cartes flash
• Tâches de représentations
• Tâches de dénombrements

Mouvements pédagogiques stratégiques
Jeux de cartes

• Cartes à nombres décimaux
• Cartes à fractions
• Cartes à nombres naturels
• Créer vos propres jeux de cartes

Remerciements

Les compétences et concepts fondamentaux en mathématiques

Les cartes de représentations et les activités suggérées sur cette page permettent aux élèves de travailler avec des nombres naturels, des fractions et/ou des nombres décimaux de différentes façons. Les activités sont conçues pour développer des compétences de sens du nombre tels que lire, compter, dénombrer, représenter, ordonner, estimer, comparer, composer, décomposer et recomposer des nombres (comprendre des faits et des opérations mathématiques). Au fur et à mesure que les élèves exécutent leurs tâches en utilisant les cartes de représentations, ils développent une compréhension des liens entre différentes représentations de la même quantité. (Mettre l'accent sur les éléments fondamentaux en mathématiques)

Activités

Jeux d'associations

1. Disposer les cartes à faces visibles. En travaillant en équipe de deux, les élèves trouvent à tour de rôle des paires correspondantes. Chaque joueur explique pourquoi les deux cartes se correspondent.
2. Disposer les cartes à face cachées, ce qui ajoute un élément de mémoire au jeu. À tour de rôle, les joueurs retournent les cartes pour trouver des paires assorties. Lorsque le joueur trouve une paire correspondante, il continue son tour à trouver une autre paire. Si les cartes ne correspondent pas, retourner les cartes à faces cachées.
3. Jouer à l'un des jeux de représentations trouvés en anglais sur la page de mathies games (jeux de mathies).
4. Jouer à "Go Fish".

Jeux de quantités et de chiffres

1. 1. Mélanger le jeu et distribuer les cartes uniformément entre les joueurs.
   2. Sans regarder les cartes, chaque joueur place sa partie du paquet face cachée dans une pile devant lui.
   3. Chaque tour est composé de tous les joueurs, chacun retournant une carte.
   4. Le joueur qui retourne la carte avec la plus grande valeur gagne toutes les cartes retournées lors de ce tour.
   5. Advenant d'une égalité lors d'une partie, un autre tour est joué.
   6. Le gagnant est le joueur qui a le plus de cartes à la fin de la partie.
2. Ordonner les cartes de la plus petite à la plus grande quantité.
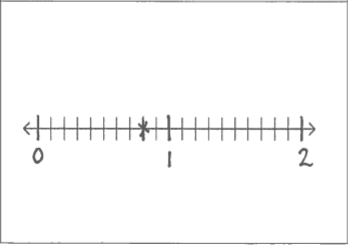
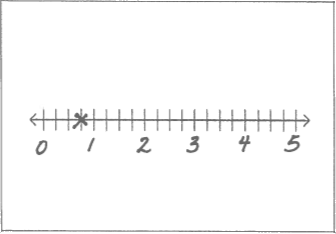
3. Placer chaque carte à l’endroit approprié sur une droite numérique.
   Commencer par placer les valeurs d'ancrage (par exemple, 0 et 1 lorsque vous travaillez avec des cartes à fractions).
   Des compétences de raisonnement proportionnel et l'habileté d'ordonner différentes valeurs sont nécessaires lorsqu'on travaille sur une droite numérique.
   

   Des élèves de Grand Erie sont engagés dans l'activité d'ordonner les nombres sur une droite numérique. Photo reproduite avec l’aimable autorisation de Beth Edwards

4. Course à l'arrivée. Choisir une valeur cible pour la ligne d'arrivée. La cible choisie dépend du type de carte sur laquelle vous travaillez (par exemple, 10, 100 ou 1,0). Chaque élève utilise une grande droite numérique segmentée avec la cible marquée. À tour de rôle, l'élève choisit une carte et la déplace autant d’unités vers la cible.
5. Retourner la carte du dessus du paquet. Cette carte est l'ancre. Retourner chacune des autres cartes une à la fois et décider si la carte est moins que, plus que, ou égale à la valeur d'ancrage.

Retour en haut

Cartes Flash

1. Identifier le numéro.
2. Identifier un nombre qui est plus grand que, ou moins qu'au numéro indiqué sur la carte flash.
3. Pour les cartes à fractions ou à nombres décimaux :
   
   • Identifier un nombre équivalent à la valeur donnée.
   • Identifier le nombre de parties nécessaires pour faire un tout (parties non ombrées).
   • Identifier le fait mathématique qui crée un tout. Partager comment la représentation aide à voir ce fait.
     
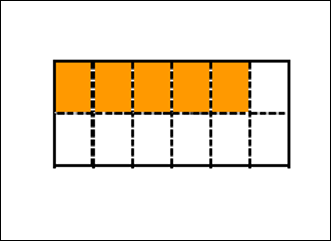
     Ce modèle de surface, par exemple, montre la fraction 5/12 en orange. Il montre également 7/12 du rectangle en blanc.
     Donc, un fait mathématique possible serait 5/12 + 7/12 = 1
4. Pour les cartes à nombres naturels :
   
   • Pour les cartes à un chiffre, identifier combien il en faut pour en faire 10.
   • Pour les cartes à deux chiffres, indiquer le nombre de dizaines et d'unités qui composent le nombre.
   • Énoncer un fait mathématique qui utilise la valeur donnée.

Tâches de représentations

1. Choisir une carte de la pile. Représenter la valeur de nombreuses façons.
   Les représentations peuvent être dessinées à la main ou créées à l'aide du matériel concret ou numérique (p. ex., outils de mathies). Les représentations pourraient être affichées en utilisant un cercle de concept ou un autre organisateur graphique.
   

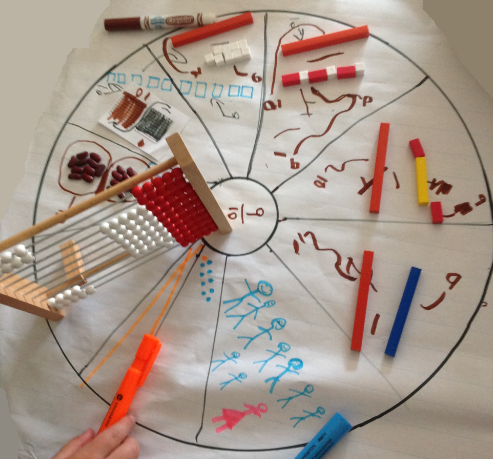
   Cercle de concept qui montre les représentations de trois quarts Photo reproduite avec l’aimable autorisation de Beth Edwards, Grand Erie DSB	Cercle de concept qui montre les représentations de neuf dixièmes Photo reproduite avec l’aimable autorisation de Beth Edwards, Grand Erie DSB

2. Choisir une carte à nombres écrits en lettres. Créer des cartes qui représentent ce nombre de différentes façons.
3. Choisir un nombre qui n’est pas actuellement dans le jeu de cartes. Créer des cartes de représentations à ajouter au jeu de cartes.

Les élèves peuvent utiliser les cartes vierges fournies ci-dessous pour ces tâches de représentations.

Tâches de dénombrements

1. Choisir une carte. Identifier le numéro et comment vous le savez.
2. Pour les cartes à fractions :
   
   • Nommer la fraction unitaire.
   • Nommer une fraction équivalente.
   • Compter en utilisant la fraction unitaire.
3. Pour les cartes à nombres naturels, compter par intervalles par la valeur indiquée sur la carte.

Retour en haut

Mouvements pédagogiques stratégiques

Pendant que les élèves jouent aux différents jeux, les enseignantes et les enseignants :

• Encouragent les élèves à expliquer leurs pensées les uns aux autres tout en jouant.
• Écoutent la discussion pour savoir la compréhension des élèves, y compris une compréhension partielle ou les malentendus.
• Cherchent des occasions d'encourager les élèves à poser des questions, à discuter, à contester et à prouver.

Idées de différenciation

• Modifier le nombre de jeux de cartes (types de représentations) avec lesquels les élèves travaillent.
• Utiliser les cartes sélectionnées dans chaque paquet. Par exemple, inclure les cartes montrant les moitiés ou les quatrièmes seulement.
• Offrir un choix en utilisant différentes activités dans divers centres.

Suggestion: imprimer chaque paquet de cartes sur une couleur différente de papier cartonné pour faciliter la séparation des ensembles de jeux.

Les élèves de 4e de Grand Erie DSB sont impliqués dans des activités d'associations. Photo gracieuseté de Beth Edwards

Retour en haut

Jeux de cartes

Chaque jeu de cartes fournit un certain type de représentation pour le même ensemble de valeurs.

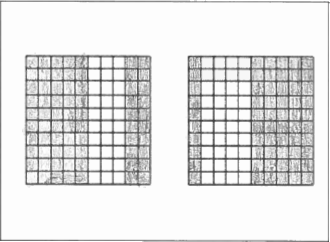
Cartes à nombres décimaux

Jeux de cartes	Échantillons
Grilles : Dixièmes ** Centièmes **
L'argent **
Droites numériques **
Cartes à nombres décimaux : Dixièmes*** Centièmes***
Cartes à fractions : Dixièmes ** Nombres fractionnaires **
Pourcentage **
Nombres décimaux écrits en lettres : Dixièmes*** Centièmes***

Retour en haut

Cartes à fractions

Ensemble #1 : fractions propres, fractions impropres et nombres fractionnaires
(Inspiré par l'activité 'Fraction Desktop')

Jeux de cartes	Échantillons
Jeu d'association : les fractions * (Cartes à droites numériques et à modèle de surface)
Droites numériques additionnelles **
Cartes numériques à fractions **
Fractions écrites en lettres***

Retour en haut

Ensemble #2 : fractions propres
(Inspiré par 'mathies Fraction Card Game')

Jeux de cartes	Échantillons
Cartes à fractions par mathies*** (l'aire, l'ensemble, la mesure et les cartes numériques)
Droites numériques **
Fractions propres écrites en lettres***

Remarquer :
Les droites numériques de fractions ont un ensemble dont la longueur varie d’une carte à l’autre. Ces cartes sont utiles pour comprendre la relation partie-tout.
Si l'objectif est de comparer des fractions, il peut être préférable de créer un ensemble de cartes à droites numériques où le tout a une longueur constante. Ce serait un bon exercice pour les élèves.

Retour en haut

Cartes à nombres naturels

Remarquer, ces cartes sont également utilisées pour certaines activités* (disponibles en anglais seulement) de numération et sens du nombre (WINS).

Jeux de cartes	Échantillons
Dés 0 jusqu'à 20
Doigts 0 jusqu'à 20
Points aléatoires 0 jusqu'à 20
Perles de Rekenrek 0 jusqu'à 50
Cartes numérotées 0 jusqu'à 50 (Quatre jeux de couleurs)
Marques de pointage 0 jusqu'à 50
Cadres à dix cases 0 jusqu'à 50

Retour en haut

Créer vos propres jeux de cartes

Les élèves peuvent également créer et jouer à leur propre jeu de cartes.
Voici quelques cartes vierges pour vous aider à démarrer.

Jeux de cartes	Échantillons
Cartes vierges **
Droites numériques vierges **
Grilles vierges de dixièmes **
Grilles vierges de centaines/centièmes **

Retour en haut

Remerciements

*Ministère de l'éducation de l'Ontario (2017). BLM 1 de l'activité Desktop Fractions peut être retrouvé dans le document interactif Fractions Learning Pathways (Unit B).
Le Parcours d'apprentissage : Les Fractions peut être accédé en français cependant, il n'est pas interactif.

**Les cartes ont été créées par Beth Edwards, conseillère pédagogique de la division junior, conseil scolaire du district de Grand Erie.
Beth travaille dans les salles de classe de 3^e, 4^e et 5^e années pour aider les élèves à établir des liens entre diverses représentations de fractions et de nombres décimaux. Elle a utilisé à la fois le jeu Fraction Card Game, touvé sur la page mathies Games ainsi que Desktop Fraction Cards à partir du document Fractions Learning Pathways (Unit B). Pour chaque jeu de cartes, Beth a ajouté des représentations supplémentaires (nombres écrits en lettres, droites numériques, pourcentages, etc.) qu'elle souhaitait utiliser avec les élèves. Elle a également créé des cartes vierges afin que les élèves puissent créer leurs propres jeux de cartes. Beth dit : "Les élèves ont adoré travailler avec les cartes." Elle recommande d’imprimer chaque paquet sur une couleur différente de papier cartonné pour faciliter la séparation des ensembles de jeux. Merci d'avoir partagé Beth!

***Remarquer que les jeux de cartes, y compris du texte anglais ont été traduites en français et les cartes à nombres décimaux ont été modifiés pour la facilité de l'utilisateur.